В топологическом пространстве.
Одним из важнейших понятий топологии является понятие окрестности.
Определение. Окрестностью точки x в топологическом пространстве (X, t) называется любое множество A, которое вместе с точкой x содержит некоторое непустое открытое множество B, содержащее точку x.
Примеры: 1.Если t - антидискретная топология на X, то для любой точки из X единственной окрестностью является все множество X.
2.Если t - дискретная топология на X, то для любой точки из X окрестностью является любое множество из X, содержащее эту точку.
Теорема 1. Множество открыто тогда и только тогда, когда оно содержит окрестность каждой своей точки.
Доказательство. Пусть A - открыто. Тогда оно содержит само себя, как окрестность любой своей точки.
Пусть теперь множество A содержит окрестность каждой своей точки, т.е., для каждой точки xÎA существует открытое множество Ux такое, что xÎUxÌA. Рассмотрим множество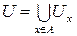 
. Очевидно, что это множество открыто. С другой стороны, оно совпадает с множеством A. Следовательно, A - открыто.ÿ
Следствие. Множество открыто тогда и только тогда, когда оно является окрестностью каждой своей точки.
Определение. Точка x называется внутренней точкой множества A, если у нее существует окрестность, целиком принадлежащая множеству A. Множество всех внутренних точек называется внутренностью множества A и обозначается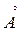 
или int A (Int A).
Определение. Точка x называется точкой прикосновения множества A, если любая окрестность точки x пересекается с множеством A. Множество всех точек прикосновения множества называется замыканием этого множества и обозначается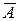 
.
Определение. Точка x называется точкой накопления или предельной точкой множества A, если любая ее окрестность содержит хотя бы одну точку множества A, отличную от точки x.
Определение. Точка x называется граничной точкой множества A, если любая ее окрестность пересекается как с множеством A, так и с его дополнением. Множество всех граничных точек множества A называется его границей и обозначается bond(A), или b(A), или гр(A).
Другими словами, граничная точка – это точка прикосновения одновременно для множества A и для его дополнения CXA.
Определение. Точка x называется внешней точкой множества A, если существует окрестность точки x не пересекающаяся с A.
Пример.Рассмотрим евклидову плоскость. В качестве топологии рассмотрим множество всех открытых кругов этой плоскости. На плоскости возьмем фигуру, изображенную на рис. 1а: заполненный ромб с «хвостом» из последовательности точек, лежащих на продолжении диагонали ромба так, что расстояние между n-ой и (n+1)-ой точками в два раза меньше расстояния между (n-1)-ой и n-ой точками. Пусть A - множество всех точек описанной фигуры. Тогда см. рис.
Теорема 1. Множество открыто тогда и только тогда, когда оно совпадает со своей внутренностью.
Теорем 2. Множество замкнуто тогда и только тогда, когда оно совпадает со своим замыканием.
Теорема 3. .
База топологии
Задание топологии перечислением открытых множеств весьма громоздко даже для конечных множеств и топологий с небольшим числом элементов. Поэтому используют менее громоздкий способ задания топологии с помощью ее базы.
Определение. Система B открытых множеств топологического пространства (X, t) называется базой топологии t, если любое открытое в этой топологии множество можно представить в виде объединения элементов этого семейства.
Любая топология является собственной базой.
Пример. Семейство всех открытых интервалов в естественной топологии числовой прямой является базой этой топологии.
Теорема 1. Семейство B открытых множеств является базой топологии t тогда и только тогда, когда для каждой точки x пространства (X, t) и любой ее окрестности W существует такой элемент U из B, что xÎUÌ W.
Доказательство.Пусть B - база топологии t. Так как W - окрестность точки x, то существует открытое множество Ux такое, что xÎUxÌW. Так как B - база, то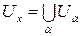 
и, следовательно, найдется такой элемент UÎB , что xÎUÌW.
С другой стороны, пусть теперь W - открытое множество. Так как оно является окрестностью каждой своей точки, то для любой точки xÎW найдется UxÎB такое, что xÎUxÌW. Рассмотрим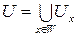 
. Очевидно, что U=W. Следовательно, произвольное открытое множество есть объединение элементов из B, то есть, B - база топологии. ÿ
Определение. Топологическое пространство называется пространством со счетной базой, если его топология имеет хотя бы одну счетную базу.
Пример. Рассмотрим естественную топологию числовой прямой и семейство B открытых интервалов с рациональными концами: B={(r,q)| r,qÎQ, r<q}. Семейство B всех открытых интервалов с рациональными концами является базой естественной топологии числовой прямой. Эта база естественной топологии поля вещественных чисел состоит из счетного числа элементов.
Теорема (признак базы). Пусть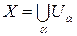 
. Покрытие B={Ua} является базой некоторой топологии t на X тогда и только тогда, когда для любых двух элементов Ua и Ub из B и каждого xÎUaÇUb существует такое Ug, что xÎUgÌUaÇUb.
Доказательство. Если B={Ua} – база топологии, то UaÇUb - открытое множество и по определению базы для каждого xÎUaÇUb существует такое Ug, что xÎUgÌUaÇUb.
Пусть теперь t - семейство всевозможных объединений множеств из B. Покажем, что t - топология с базой B. Действительно, выполнимость аксиом 1, 2 и 4 топологического пространства в рассматриваемом случае очевидна. Остается показать, что аксиома 3 тоже выполняется. Пусть Ua и Ub принадлежат t. Тогда для любой точки xÎ UaÇUb найдутся такие Ux и Vx из B, что xÎUxÇVx . Но тогда по условию теоремы найдется элемент Ug из B такой, что xÎUgÌUxÇVxÌ UaÇUb. Рассмотрим множество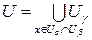 
. Очевидно, что Ug=UaÇUb и что UgÎt. Таким образом, аксиома 3 для t выполняется, t является топологией, а B - ее базой. ÿ
Теорема (построение базы). Пусть G - произвольное непустое семейство множеств. Тогда семейство B всевозможных пересечений элементов из G взятых в конечном числе является базой некоторой топологии t на множестве
X=È S | S Î G.
Эта теорема позволяет определять, является ли некоторое покрытие множества X базой топологии на этом множестве или нет.
Теорема (признак базы уже имеющейся топологии). Семейство открытых множеств в топологии t является базой этой топологии тогда и только тогда, когда пересечение любых двух элементов этого семейства можно представить в виде объединения элементов этого же семейства.
Определение. Семейство G открытых в топологическом пространстве X множеств называется предбазой топологии на X, если множества, являющиеся пересечением всевозможных конечных систем из G, образуют базу пространства X.
Теорема 4. Предбаза является базой некоторой топологии, если пересечение любых двух элементов этой предбазы можно представить в виде объединения элементов этой же предбазы.
Дата добавления: 2016-06-02; просмотров: 2438;