Непрерывные отображения. Гомеоморфизмы
Определение. Отображение f топологического пространства (X,t) в другое (X¢,t¢) называется непрерывным в точке xÎX, если для любой окрестности Uf(x) точки f(x) найдется такая окрестность VxÎt точки x, что ее образ целиком лежит в Uf(x), т.е. f(Vx)ÌUf(x).
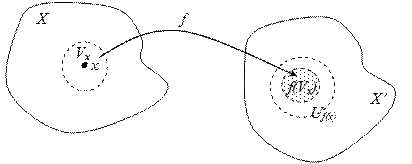Определение. Отображение f: (X,t) ® (X¢,t¢) называется непрерывным, если оно непрерывно в каждой точке пространства X.
Определение. Отображение f: (X,t) ® (X¢,t¢) называется открытым, если прообраз каждого открытого множества открыт.
Теорема 1. Отображение f: (X,t) ® (X¢,t¢) непрерывно тогда и только тогда, когда оно открыто.
Доказательство.
1. Пусть f непрерывно. Возьмем некоторое открытое множество VÎt и найдем его полный прообраз UÌ X. Для каждой точки xÎU очевидно f(x)ÎV, так как V открыто, то оно является окрестностью каждой своей точки f(x). Из определения непрерывного отображения следует, что у точки x найдется окрестность Ux, целиком лежащая в U такая, что f(Ux)ÌV. Рассмотрим множество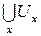 
для xÎU. Очевидно, оно открыто и совпадает с U. Следовательно, отображение f является открытым.
2. Пусть отображение f открыто и x - произвольная точка пространства X. Выберем произвольную окрестность V точки f(x), тогда ее полный прообраз UÌX является открытым и окрестностью точки x, причем f(U)=VÍV т.е. выполняются все требования определения непрерывности отображения в точке x. Так как точка x выбрана произвольно, то отображение f непрерывно. ÿ
Следствие. Отображение непрерывно тогда и только тогда, когда прообраз любого замкнутого множества замкнут.
Примеры: 1. Тождественное преобразование является непрерывным отображением.
2.Любое движение, любое подобие является непрерывным отображением.
Для доказательства достаточно показать, что в рассматриваемых случаях каждое открытое множество можно представить в виде объединения элементов базы (открытых шаров или открытых параллелепипедов).
3.Инверсия не является непрерывным отображением.
Определение. Отображение одного топологического пространства в другое называется гомеоморфизмом, если оно биективно (взаимно однозначно) и непрерывно в обе стороны.
Пример.y=ax+b гомеоморфизм R®R или R®(x;y)ÎR2 (числовой прямой в график функции).
Определение. Два пространства (X,t) и (X¢,t¢) называются гомеоморфными, если существует гомеоморфизм f: (X,t) ® (X¢,t¢).
Примеры: 1. Интервал гомеоморфен прямой.
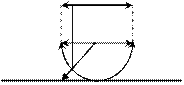2.Открытый круг гомеоморфен плоскости.
3.n–мерное евклидово пространство гомеоморфно n–мерным аффинному и арифметическому пространствам.
Замечание. Отношение гомеоморфизма на множестве всех топологических пространств является отношением эквивалентности.
Из определения гомеоморфизма следует, что он сохраняет открытые множества, т.е. открытые множества являются его инвариантами. Более того, гомеоморфизм устанавливает взаимно однозначное соответствие не только между точками топологических пространств, но и между элементами их топологий. Поэтому два гомеоморфных пространства эквивалентны с топологической точки зрения, т.е. имеют одинаковые свойства.
Дата добавления: 2016-06-02; просмотров: 2073;