Дискретные и непрерывные случайные величины
Рассматривая случайные события, сталкивались с такими, которые состоят в появлении того или иного числа. Например, при бросании игрального кубика выпавшие очки выражаются числом от 1 до 6. Наперед определить какое именно число появится в результате опыта невозможно. В этом смысле число выпавших очков при бросании кубика есть величина случайная (СВ). Случайная величина является количественной характеристикой случайного результата опыта.
Определение. Случайной величинойназывается величина, которая в результате опыта может принимать то или иное числовое значение, причем заранее неизвестно какое именно.
Обозначают
· случайные величины заглавными буквами латинского алфавита: X, Y, Z, U, V …
· значения случайных величин малыми буквами с индексами: x1, x2,…y1, y2,…
Примеры случайных величин:
1) X – число попаданий в мишень при двух выстрелах;
возможные значения этой СВ: x1 = 0 (нет ни одного попадания), x2 = 1 (одно попадание), x3 = 2 (два попадания).
2) Y – рост случайно выбранного человека;
Возможные значения СВ Y перечислить нельзя, можно лишь указать промежуток, которому эти значения принадлежат: ymin – ymax.
Примеры 1) и 2) показывают, что случайные величины можно разделить на две категории: те, которые принимают отдельные, изолированные значения на числовой прямой и те, которые заполняют некоторый промежуток на числовой прямой. Эти категории образуют Дискретные и Непрерывные случайные величины.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать счетное, хотя и бесконечное количество значений.
Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
§2. Закон распределения дискретной случайной величины.
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.
Решение:
Найдем вероятности пяти попаданий из пяти возможных, четырех из пяти, трех из пяти, двух из пяти, одного из пяти и нуля из пяти по формуле Бернулли:
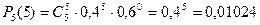 ,
, 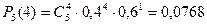 ,
, 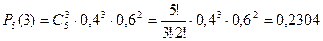 ,
, 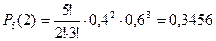
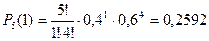
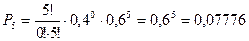
Проверим, что сумма вероятностей равна единице:
0,01024+0,0768+0,2304+0,3456+0,2592+0,07776=1.
Запишем ряд (таблицу) распределения СВ:
| X | ||||||
| p | 0,07776 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,01024 |
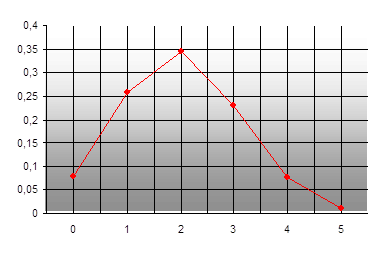 |
Представим графически зависимость числа попаданий от их вероятностей.
При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.
§3. Функция распределения случайной величины.
Задание случайной величины путем определения значений этой величины и вероятностей этих значений применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. P(Х < x), обозначим через F(x).
Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее аргумента х.
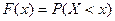
Функцию распределения также называют интегральной функцией.
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:
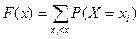
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Так, построим функцию распределения для примера, рассмотренного в §2:

 Если х ≤ 0, то значений случайной величины, меньше такого х нет, т.е. P(X<x) = 0;
Если х ≤ 0, то значений случайной величины, меньше такого х нет, т.е. P(X<x) = 0;
Если 0 < x ≤ 1, то меньше такого х только одно значение: x1 = 0 и его вероятность
P(X<x) = 0,07776.
Если 1 < x ≤ 2, то меньше такого х только два значения: x1 = 0 и x2 = 1, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0 и x2 = 1:
P(X<x) = 0,07776 + 0,2592 = 0,33696.
Если 2 < x ≤ 3, то меньше такого х три значения: x1 = 0, x2 = 1 и х3 =2, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0, x2 = 1, х3 =2:
P(X<x) = 0,07776 + 0,2592 + 0,3456 = 0,68256.
Если 3 < x ≤ 4, то меньше такого х четыре значения: x1 = 0, x2 = 1, х3 =2 и х4 = 3, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0, x2 = 1, х3 =2, х4 = 3:
P(X<x) = 0,07776 + 0,2592 + 0,3456 + 0,2304 = 0,91296.
Если 4 < x ≤ 5, то меньше такого х пять значений: x1 = 0, x2 = 1, х3 =2, х4 = 3,х5 = 4, вероятность того, что X<x будет равна для таких х сумме вероятностей значений x1 = 0,
x2 = 1, х3 =2, х4 = 3, х5 = 4:
P(X<x) = 0,07776 + 0,2592 + 0,3456 + 0,2304 + 0,0768 = 0,98976.
Если x > 5, то меньше такого х все шесть значений: вероятность того, что X<x будет равна для таких х сумме всех вероятностей:
P(X<x) = 0,07776 + 0,2592 + 0,3456 + 0,2304 + 0,0768 + 0,01024 =1.
Таким образом, запишем функцию распределения:
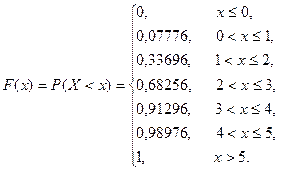
Построим ее график:

Функция распределения дискретной случайной величины Х разрывная и возрастает скачками при переходе через каждое значение хi.
Для непрерывной СВ функция распределения является непрерывной.
§4.Свойства функции распределения.
1) значения функции распределения принадлежат отрезку [0, 1].
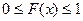
2) F(x) – неубывающая функция:
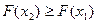 при
при 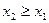
3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале:
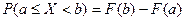
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице:
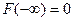 ,
, 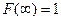 .
.
5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю:
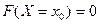 , если X – непрерывная случайная величина.
, если X – непрерывная случайная величина.
Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.
§5. Плотность распределения.
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси, т.е., по ней невозможно определить какое из значений непрерывной случайной величины более возможно, а какое менее. В этой связи вводится еще одна функция, характеризующая распределение случайной величины.
Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется первая производная от функции распределения F(x):
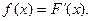
функция f(x) – плотность распределения вероятностей.
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприменима.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
Определение.Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением, может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность с которой некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.

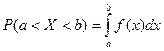
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми
x = a и x = b.
 Функция распределения может быть найдена, если известна плотность распределения, по формуле:
Функция распределения может быть найдена, если известна плотность распределения, по формуле:
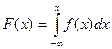
§6. Свойства плотности распределения.
1) Плотность распределения – неотрицательная функция.
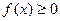
2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.
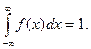
Пример 1. Случайная величина подчинена закону распределения с плотностью:
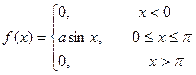
Требуется найти коэффициент а, построить график плотности вероятностей и определить вероятность того, что случайная величина попадет в интервал от 0 до 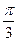 .
.
Решение:
Для нахождения коэффициента а воспользуемся свойством 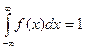 .
.
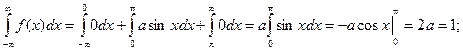
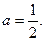
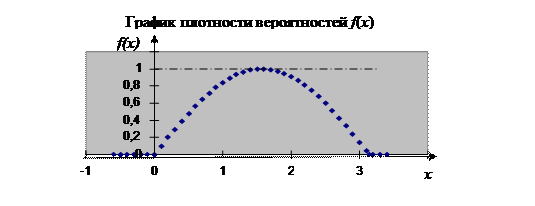
Находим вероятность попадания случайной величины в заданный интервал.
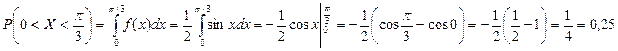
§6. Числовые характеристики случайных величин.
Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение (центр), вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.
Математическое ожидание.
Наиболее распространенной характеристикой центра распределения значений случайной величины является математическое ожидание.
Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.
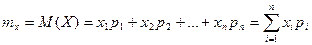
Определение. Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл на этом отрезке от произведения переменной х на плотность вероятностей f(x):

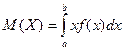
Если возможные значения непрерывной случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

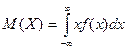
С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания.
1) Математическое ожидание постоянной величины равно самой постоянной.
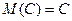
2) Постоянный множитель можно выносить за знак математического ожидания.
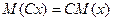
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
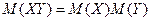
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
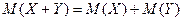
Это свойство также справедливо для произвольного числа случайных величин.
Дисперсия.
Математическое ожидание не может полностью характеризовать случайную величину. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.
Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.
Определение. Дисперсией (рассеиванием) случайной величины (и дискретной и непрерывной) называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
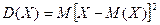
Дисперсия дискретной сл. величины задается формулой:
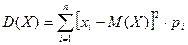
Дисперсия непрерывной сл. величины определяется так:
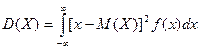
Замечание: При этом предполагается, что несобственный интеграл сходится.
Однако, на практике подобный способ вычисления дисперсии не всегда удобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям.
Поэтому применяется другой способ.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.
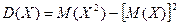
Т.о., для дискретной сл. величины формула для вычисления дисперсии такова:
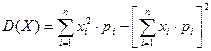 ,
,
для практического вычисления дисперсии непрерывной сл. величины используется формула:
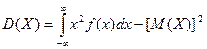
Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю.
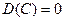
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
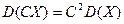
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
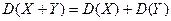
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
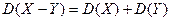
Справедливость этого равенства вытекает из свойства 2.
Среднее квадратическое отклонение
Дисперсия имеет размерность, равную квадрату размерности сл. величины. В задачах практики часто бывает нужно оценить рассеяние значений сл. величины относительно среднего значения в единицах самой сл. величины. Для этого вводят еще одну характеристику рассеяния – среднее квадратическое отклонение.
Определение. Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии.

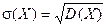
| <== предыдущая лекция | | | следующая лекция ==> |
| Вероятность того, что деталь находится только в одном ящике, равна | | | Физиология бактерий. Питание бактерий. Ферменты. |
Дата добавления: 2016-05-25; просмотров: 5826;
