Аналоговые, дискретные и цифровые сигналы

ВВЕДЕНИЕ В ЦИФРОВУЮ ОБРАБОТКУ СИГНАЛОВ

Цифровая обработка сигналов (ЦОС или DSP - digital signal processing) является одной из новейших и самых мощных технологий, которая активно внедряется в широкий круг областей науки и техники, таких как коммуникации, метеорология, радиолокация и гидролокация, медицинская визуализация изображений, цифровое аудио- и телевизионное вещание, разведка нефтяных и газовых месторождений и др. Можно сказать, что происходит повсеместное и глубокое проникновение технологий цифровой обработки сигналов во все сферы деятельности человечества. Сегодня технология ЦОС относится к числу базовых знаний, которые необходимы ученым и инженерам всех отраслей без исключения.

Сигналы

Что такое сигнал? В наиболее общей формулировке это зависимость одной величины от другой. Т.е., с математической точки зрения сигнал является функцией. Чаще всего рассматриваются зависимости от времени. Физическая природа сигнала может быть различной. Очень часто это электрическое напряжение, реже – ток.

Формы представления сигнала:

1. временная;

2. спектральная (в частотной области).

Стоимость цифровой обработки данных меньше аналоговой и продолжает снижаться, а производительность вычислительных операций непрерывно возрастает. Немаловажным является и то, что системы ЦОС отличаются высокой гибкостью. Их можно дополнять новыми программами и перепрограммировать на выполнение различных операций без изменения оборудования. Поэтому интерес к научным и к прикладным вопросам цифровой обработки сигналов возрастает во всех отраслях науки и техники.

ПРЕДИСЛОВИЕ К ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ

Дискретные сигналы

Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и др.) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в ВУ.

Аналоговые, дискретные и цифровые сигналы

Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты t, называются аналоговыми.

Какой сигнал называется цифровым? Рассмотрим некоторый аналоговый сигнал (рис. 1.1 а). Он задан непрерывно на всем рассматриваемом временном интервале. Считается, что аналоговый сигнал абсолютно точен, если не учитывать погрешности при измерении.

Рис. 1.1 а) Аналоговый сигнал

Рис. 1.1 б) Дискретизированный сигнал

Рис. 1.1 в) Квантованный сигнал

Для того, чтобы получить цифровой сигнал, нужно провести две операции – дискретизацию и квантование. Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией, а результат такого преобразования - дискретным сигналом.Т. обр., дискретизация заключается в составлении выборки из аналогового сигнала (рис. 1.1 б), каждый элемент которой, называемый отсчетом, будет отстоять по времени от соседних отсчетов на некотором интервале Т, называемом интервалом дискретизации или (поскольку интервал дискретизации чаще неизменен) – периодом дискретизации. Величина, обратная периоду дискретизации называется частотой дискретизации и определяется как:

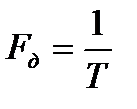(1.1)

При обработке сигнала в вычислительном устройстве его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием. Возникающие при этом ошибки округления называются ошибками или шумами квантования. Т. обр., квантование – это приведение уровней дискретизированного сигнала к некоторой сетке (рис. 1.1 в), чаще обычным округлением в сторону большего. Дискретный во времени и квантованный по уровню сигнал и будет являться цифровым.

Условия, при которых возможно полное восстановление аналогового сигнала по его цифровому эквиваленту с сохранением всей исходно содержавшейся в сигнале информации, выражаются теоремами Найквиста, Котельникова, Шеннона, сущность которых практически одинакова. Для дискретизации аналогового сигнала с полным сохранением информации в его цифровом эквиваленте максимальные частоты в аналоговом сигнале должны быть не менее, чем вдвое меньше, чем частота дискретизации, то есть f_max £ (1/2)f_d, т.е. на одном периоде максимальной частоты должно быть минимум два отсчета. Если это условие нарушается, в цифровом сигнале возникает эффект маскирования (подмены) действительных частот более низкими частотами. При этом в цифровом сигнале вместо фактической регистрируется "кажущаяся" частота, а, следовательно, восстановление фактической частоты в аналоговом сигнале становится невозможным. Восстановленный сигнал будет выглядеть так, как если бы частоты, лежащие выше половины частоты дискретизации, отразились от частоты (1/2)f_d в нижнюю часть спектра и наложились на частоты, уже присутствующие в этой части спектра. Этот эффект называется наложением спектров или алиасингом (aliasing). Наглядным примером алиасинга может служить иллюзия, довольно часто встречающаяся в кино – колесо автомобиля начинает вращаться против его движения, если между последовательными кадрами (аналог частоты дискретизации) колесо совершает более чем пол-оборота.

Преобразование сигнала в цифровую форму выполняется аналого-цифровыми преобразователями (АЦП). Как правило, они используют двоичную систему счисления с определенным числом разрядов в равномерной шкале. Увеличение числа разрядов повышает точность измерений и расширяет динамический диапазон измеряемых сигналов. Потерянная из-за недостатка разрядов АЦП информация невосстановима, и существуют лишь оценки возникающей погрешности «округления» отсчетов, например, через мощность шума, порождаемого ошибкой в последнем разряде АЦП. Для этого используется понятие отношения «сигнал/шум» - отношение мощности сигнала к мощности шума (в децибелах). Наиболее часто применяются 8-, 10-, 12-, 16-, 20- и 24-х разрядные АЦП. Каждый дополнительный разряд улучшает отношение сигнал/шум на 6 децибел. Однако увеличение количества разрядов снижает скорость дискретизации и увеличивает стоимость аппаратуры. Важным аспектом является также динамический диапазон, определяемый максимальным и минимальным значением сигнала.

Обработка цифровых сигналов выполняется либо специальными процессорами, либо на универсальных ЭВМ и компьютерах по специальным программам. Наиболее просты для рассмотрения линейные системы. Линейными называются системы, для которых имеет место принцип суперпозиции (отклик на сумму входных сигналов равен сумме откликов на каждый сигнал в отдельности) и однородность (изменение амплитуды входного сигнала вызывает пропорциональное изменение выходного сигнала).

Если входной сигнал x(t-t₀) порождает однозначный выходной сигнал y(t-t₀) при любом сдвиге t₀, то систему называют инвариантной во времени. Ее свойства можно исследовать в любые произвольные моменты времени. Для описания линейной системы вводится специальный входной сигнал - единичный импульс (импульсная функция).

Единичный импульс (единичный отсчет) u₀(n) (рис. 1.2):

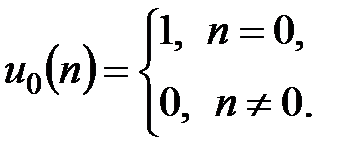
Рис. 1.2. Единичный импульс

В силу свойства суперпозиции и однородности любой входной сигнал можно представить в виде суммы таких импульсов, подаваемых в разные моменты времени и умноженных на соответствующие коэффициенты. Выходной сигнал системы в этом случае представляет собой сумму откликов на эти импульсы. Отклик на единичный импульс (импульс с единичной амплитудой) называют импульсной характеристикой системыh(n). Знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Действительно, произвольный сигнал {x(n)} можно представить в виде линейной комбинации единичных отсчетов:

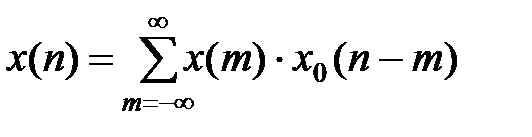(1.2)

Выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик:

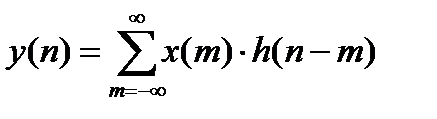(1.3)

Это выражение называется дискретной сверткой. Краткая запись: 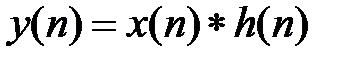. (1.4)

Z-преобразование

Для анализа дискретных сигналов и систем, кроме свертки, широко используется z-преобразование и дискретное преобразование Фурье (ДПФ).

Удобным способом анализа дискретных последовательностей является z-преобразование. Смысл его заключается в том, что последовательности чисел 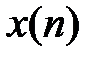ставится в соответствие функция комплексной переменной z, определяемая следующим образом:

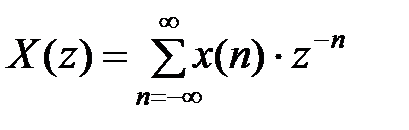(1.5)

Z-преобразование можно рассматривать как способ однозначного представления последовательности 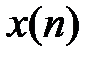в комплексной z-плоскости.

Это преобразование позволяет использовать всю мощь дифференциального и интегрального исчисления дискретной математики, алгебры и прочих хорошо развитых разделов аналитической математики.

Отображение z-преобразования выполняют на комплексной z-плоскости с Re z и Im z по осям координат (рис. 1.3). В частности, спектральной оси частот на z-плоскости соответствует окружность радиуса

|z|= 1.

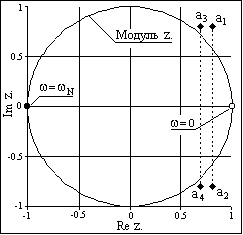
Рис.1.3. Комплексная z-плоскость