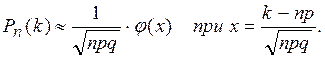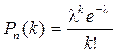Вероятность того, что деталь находится только в одном ящике, равна
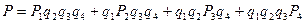
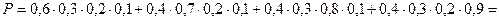
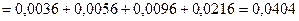
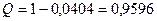
Вероятность того, что нужной деталь нет ни в одном ящике, равна:
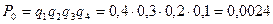
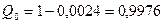
Искомая вероятность равна 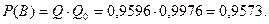
§7. Формула полной вероятности.
Пусть некоторое событие А может произойти вместе с одним из несовместных событий 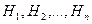 , составляющих полную группу событий. Пусть известны вероятности этих событий
, составляющих полную группу событий. Пусть известны вероятности этих событий 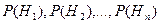 и условные вероятности наступления события А при наступлении события Hi
и условные вероятности наступления события А при наступлении события Hi 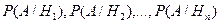 .
.
 Теорема. Вероятность события А, которое может произойти вместе с одним из событий
Теорема. Вероятность события А, которое может произойти вместе с одним из событий 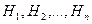 , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
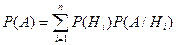
Фактически эта формула полной вероятностиуже использовалась при решении примеров, приведенных выше, например, в задаче с револьвером.
Доказательство.
Т.к. события 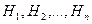 образуют полную группу событий, то событие А можно представить в виде следующей суммы:
образуют полную группу событий, то событие А можно представить в виде следующей суммы:
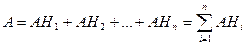
Т.к. события 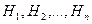 несовместны, то и события AHi тоже несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий:
несовместны, то и события AHi тоже несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий:
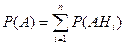
При этом 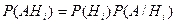
Окончательно получаем: 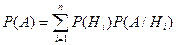
Теорема доказана.
Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.
Решение.
Вероятность того, что выстрелы производит первый, второй или третий стрелок равна 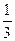 .
.
Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
- для первого стрелка: 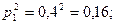
- для второго стрелка: 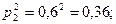
- для третьего стрелка: 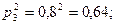
Искомая вероятность равна:
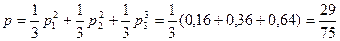
§8. Формула Бейеса. (формула гипотез)
Пусть имеется полная группа несовместных гипотез 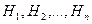 с известными вероятностями их наступления
с известными вероятностями их наступления 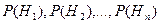 . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности 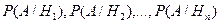 .
.
Требуется определить какие вероятности имеют гипотезы 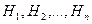 относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности 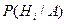 .
.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

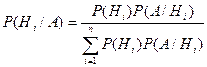
Эта формула называется формулой Бейеса.
Доказательство.
По Теореме умножения вероятностей получаем:
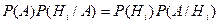
Тогда если 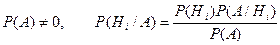 .
.
Для нахождения вероятности P(A) используем формулу полной вероятности.
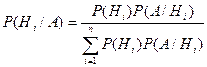
Если до испытания все гипотезы равновероятны с вероятностью 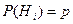 , то формула Бейеса принимает вид:
, то формула Бейеса принимает вид:

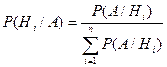
§9. Повторение испытаний.
Формула Бернулли.
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.
Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рn,(k) того, что в результате п испытаний событие А наступило ровно k раз.
Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако при достаточно большом количестве испытаний это приводит к громоздким вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик)
Пусть в результате п независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие 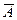 с вероятностью
с вероятностью 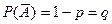 .
.
Обозначим Ai – наступление события А в испытании с номером i. Т.к. условия проведения опытов одинаковые, то эти вероятности равны.
Если в результате п опытов событие А наступает ровно k раз, то остальные п-k раз это событие не наступает. Событие А может появиться k раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по k. Это количество сочетаний находится по формуле:
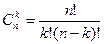
Вероятность каждой комбинации равна произведению вероятностей:
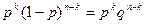
Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:

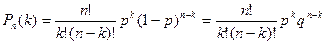
Здесь 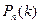 - вероятность того, что в п испытаниях событие А появиться k раз.
- вероятность того, что в п испытаниях событие А появиться k раз.
Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.
Решение.
Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.
Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в k испытаниях событие в вероятностью р наступает ровно п раз.
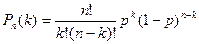
В случае пяти попаданий из пяти возможных:
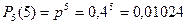
Четыре попадания из пяти выстрелов:
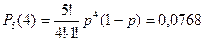
Три попадания из пяти:
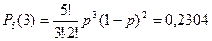
Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
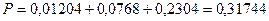
§10. Локальная и интегральная формулы Муавра-Лапласа. Формула Пуассона.
(Симеон Дени Пуассон (1781 – 1840) – французский математик)
Пусть производится пнезависимых испытаний, в которых событие А появляется с одной и той же вероятностью р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании постоянна и отлична от 0 и 1, то вычислять вероятность Pn(k) того, что в п испытаниях событие А появиться k раз по формуле Бернулли затруднительно (при больших п получаются факториалы больших чисел и большие степени вероятностей p и q). В этом случае используют приближенные формулы для определения вероятности. К ним относятся локальная формула Муавра-Лапласа и формула Пуассона. Локальная формула Муавра-Лапласа применима при npq »1 (много больше единицы, например в некоторых учебниках задается npq≥20) и k ≈ np. Эта формула имеет вид:
|
Здесь 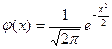 - функция Гаусса, таблица значений которой задаются в приложениях учебников по теории вероятностей. Следует заметить, что функция Гаусса является четной, т.е.
- функция Гаусса, таблица значений которой задаются в приложениях учебников по теории вероятностей. Следует заметить, что функция Гаусса является четной, т.е. 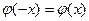 .
.
При больших п и малых р (p£0,1; npq<10) вероятность Pn(k) приближенно находится следующим образом:
Сделаем важное допущение – произведение пр сохраняет постоянное значение:
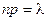 , т.е.
, т.е. 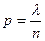 .
.
Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.
По формуле Бернулли получаем:
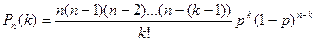
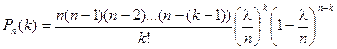
Найдем предел этой вероятности при п®¥:
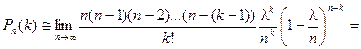
|
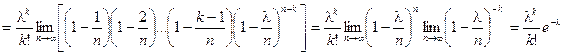
Получаем формулу Пуассона:
Если известны числа l и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.
В условиях локальной формулы Муавра-Лапласа вероятность того, что в n независимых испытаниях событие А появится не менее, чем k1 и не более, чем k2 раз (т.е. 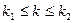 ) можно приближенно найти по интегральной формуле Муавра-Лапласа:
) можно приближенно найти по интегральной формуле Муавра-Лапласа:
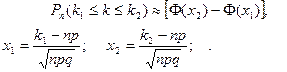
Здесь 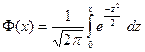 - функция Лапласа, таблица значений которой приводится в приложениях учебников по теории вероятностей. Причем,
- функция Лапласа, таблица значений которой приводится в приложениях учебников по теории вероятностей. Причем, 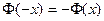 и при
и при 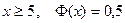 .
.
Замечание: в некоторых учебниках функция Лапласа может задаваться как 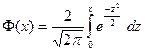 , в этом случае интегральная формула Муавра-Лапласа будет иметь вид:
, в этом случае интегральная формула Муавра-Лапласа будет иметь вид: 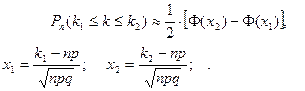 .
.
Примеры:
1. Вероятность того, что при штамповке изделий отдельное изделие окажется бракованным (т.е. с отклонением от стандарта) постоянна и равна 0,05. Найти вероятность того, что в партии из 1000 изделий окажется ровно 40 бракованных.
Решение: По условию задачи n = 1000, p = 0,05, q = 1 – 0,05 = 0,95, k = 40. Тогда, т.к. npq = = 1000·0,05·0,95 = 47,5 >20 и np = 1000·0,05 = 50 имеет один порядок с k = 40, будем использовать локальную формулу Муавра-Лапласа:
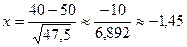 ,
, 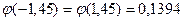 ,
, 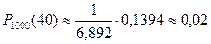 .
.
2. Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,007. Поступило 1000 вызовов. Определите вероятность 9 сбоев.
Решение: По условию задачи n = 1000, p = 0,007, q = 1 – 0,007 = 0,993, k = 9. Тогда, т.к. p < 0,1и npq = = 1000·0,007·0,993 = 6,951 <10, будем для вычисления вероятности 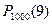 использовать формулу Пуассона:
использовать формулу Пуассона:
Имеем 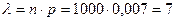 , тогда
, тогда 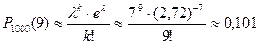 .
.
3. Вероятность попадания в цель из скорострельного орудия при одном выстреле равна 0,75. Найти вероятность того, что при 300 выстрелах число попаданий будет не менее 210, но и не более 230 раз.
Решение: По условию задачи n = 300, p = 0,75, q = 1 – 0,77 = 0,25, k1 = 210, k2 = 230. Для нахождения вероятности 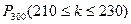 воспользуемся интегральной формулой Муавра-Лапласа. Имеем:
воспользуемся интегральной формулой Муавра-Лапласа. Имеем: 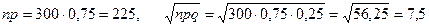 . Тогда
. Тогда 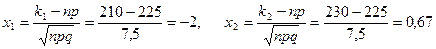 . Следовательно,
. Следовательно, 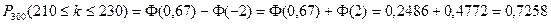 .
.
Дата добавления: 2016-05-25; просмотров: 2018;