Определение. Полной группой событий называется совокупность всех возможных результатов опыта.
Основные понятия.
Первичными в ТВ (теории вероятностей) являются понятия
· Опыт или испытание,
· Событие,
· Равновозможность событий.
Под опытом или испытанием будем понимать последовательность действий (осуществление комплекса условий), которые можно повторить сколько угодно раз.
Опыт: бросание игрального кубика; извлечение одной карты из колоды, ит.д.
Событием называется всякий факт, который может произойти или не произойти в результате опыта.
Обозначают события заглавными буквами с расшифровкой, например:
Событие А=выпало 4 очка при бросании кубика;
Событие В = извлечена карта пиковой масти.
События называются равновозможными, если нет оснований считать, что одно из них более возможно (появится в результате опыта с большей вероятностью), чем другое. В основе равновозможности событий лежат соображения симметрии и здравого смысла. Например, при бросании кубика выпадение 2 и 6 очков равновозможны, т.к. кубик однороден и симметричен, но при стрельбе по мишени попадание и промах нельзя, вообще говоря, считать равновозможными.
Тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда.
Определение. Достоверным событиемназывается событие, которое обязательно произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. Событие называется случайным, если в результате опыта оно может произойти, а может и не произойти.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие, а появление красного шара – случайное событие.
В отношении друг друга события имеют некоторые особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом – нет.
Определение. События называются несовместными, если появление одного из них исключает появление других, в противном случае события называются совместными.
Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).
Определение. Полной группой событий называется совокупность всех возможных результатов опыта.
Определение. Элементарными исходами опыта называются такие результаты опыта, которые:
1. взаимно исключают друг друга (являются попарно несовместными);
2. являются равновозможными;
3. образуют полную группу событий (в результате опыта происходит одно из этих событий);
4. каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.
Совокупность всех элементарных исходов опыта называется пространством элементарных событий.
Определение. Противоположными называются два несовместных события, образующие полную группу. Обозначают противоположные события Aи Ā
Определение. Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.
Пример: при бросании одного игрального кубика элементарными исходами будут события: «выпала 1», «выпала 2», «выпала 3», «выпала 4», «выпала 5», «выпала 6».
Для события А= выпало число очков, большее четырех, благоприятными будут события «выпала 5», «выпала 6».
§2.Классическое, статистическое и геометрическое определение вероятности события.
Подвероятностью события А понимается математическая (количественная) оценка возможности появления этого события в результате опыта.
Определение. (Классическое определение вероятности) Вероятность события Аравна отношению числа исходов опыта, благоприятствующих событию А, к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
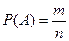
Здесь
P(A) – вероятность события А
m – число исходов опыта, благоприятствующих событию А
n – общее число исходов опыта.
Очевидно, что для достоверного события m = n, для невозможного события m = 0,для случайного события 0 < m < n. Таки образом, справедливо утверждение:
Вероятность достоверного события равна единице, вероятность невозможного – равна нулю, вероятность случайного события выражается числом, расположенным между нулем и единицей. Значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.
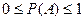
Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет
а) красным, б) зеленым, в) белым.
Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.
Число всех исходов опыта равно числу шаров, т.е. n = 10, число благоприятствующих событиям исходов соответственно равно mA =3, mB = 2, mC = 10 – 5 = 5.
Тогда, в соответствием с формулой классического определения вероятности, получаем:
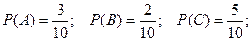
Вообще говоря, классическое определение вероятности – довольно относительное.
Это обусловлено тем, что на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные. Например, при проведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д. В этой связи вводится понятие статистической вероятности события.
Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.
W(A) =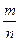 
,
W(A) – относительная частота события А; m – число опыта, в которых событие Апроизошло; n – общее число проведенных опытов.
Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Если при 12 выстрелах по мишени попадание отмечалось в 8 выстрелах, тогда, относительная частота попадания равна W(A) =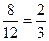 
.
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа p. Это число может быть принято за статистическую вероятность события.
Чтобы преодолеть недостаток классического определения вероятности, связанный с бесконечностью числа элементарных исходов опыта, вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства).
Введем понятие мера множества S: (обозначим Ω(S))
· Для множества точек начисловой прямой мерой является длина соответствующего числового промежутка;
· Мерой множества точек на плоскости является площадь фигуры, содержащей все эти точки;
· Мерой множества точек трехмерного пространства является объем соответствующего тела.
Так, если на отрезке AB длиной Ω(AB) = L выделен отрезок A1B1 длины Ω(A1B1) = l, то вероятность попадания наугад взятой точки в отрезок A1B1 равна отношению l/L.
Пример: Найти вероятность тог, что случайно брошенная в квадрат со стороной 4
единицы точка попадет в заштрихованную область (см. рисунок).
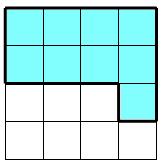
Решение: Площадь всего квадрата Ω(S) = 4·4 = 16; площадь отмеченной части Ω(s) = 9. Искомая вероятность: P = 9/16 = 0,5625.
§3. Операции над событиями.
Определение. События А и Вназываются равными, если осуществление события А влечет за собой осуществление события Ви наоборот.
Определение. Объединениемили суммой событий A1,A2,…,Аk называется событие A, которое заключается в появление хотя бы одногоиз событий Аk.
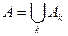= A1+A2+…+Ak
Дата добавления: 2016-05-25; просмотров: 2107;