Определение. Пересечениемили произведениемсобытий A1,A2,…, Ak называется событие А, которое заключается в осуществлении всех событий Ak.

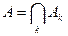= A₁·A₂·…·A_k

Замечание: Если в словесной форме между событиями произносится союз «и», то имеет место произведение событий, а если произносится союз «или», то имеет место сумма событий.

Примеры:

1. В урне находятся 5 красных, 8 зеленых, 4 желтых и 3 черных шара. Наудачу извлекают один шар. Рассмотрим события: А – извлечен цветной (не черный) шар. Очевидно, что событие А наступит, если будет извлечен красныйили зеленый или желтыйшар, т.е. имеет место сумма событий А = К + З + Ж.

2. Три стрелка делают по одному выстрелу по мишени. Рассмотрим событие В: попадут только первый и третий стрелки. Введем обозначения событий: А₁ – первый стрелок попал в мишень, тогда Ā₁ – первый стрелок не попал в мишень (промахнулся), А₂ – второй стрелок попал в мишень, Ā₂ – второй стрелок промахнулся, А₃ – третий стрелок попал в мишень, Ā₃ – третий стрелок промахнулся. Событие В произойдет, если первый стрелок попадет в мишень и второй стрелок промахнется и третий стрелок попадет,т.е. будет иметь место произведение событий: В = А₁· Ā₂· А₃.

§4. Теоремы о вероятности суммы событий.

Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

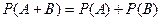
Следствие 1: Если события 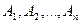образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

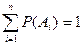
Следствие 2: Сумма вероятностей противоположных событий равна единице.

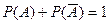
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

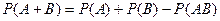
Примеры:

1) На тарелке лежат одинаковые на вид пирожки с разной начинкой: три с мясом, три с яйцом, два с яблоком и два с изюмом. Какова вероятность того, что случайно выбранный пирожок окажется со сладкой начинкой (с яблоком или с изюмом)?

Решение:

Рассмотрим события : А – извлечен пирожок с яблоком;

В – извлечен пирожок с изюмом.

Число всех исходов испытания ( выбор одного пирожка) равно числу пирожков, т.е.

n = 3 + 3 + 2 + 2 = 10; число благоприятных исходов: m_A =2, m_B = 2.

События А и В несовместные; сумма А + В и есть событие, состоящее в выборе сладкого пирожка. По теореме о вероятности сумма двух несовместных событий получим:

P(A + B) = P(A) + P(B) = 2/10 + 2/10 = 4/10 = 0,4.

2) Из колоды в 36 карт наудачу извлекают одну карту. Найти вероятность того, что это будет карта бубновой масти или туз.

Решение:

Рассмотрим события : А – извлечена карта бубновой масти;

В – извлечен туз.

Вероятности этих событий легко найти по классическому определению, т.к. m_A =9 (в колоде 9 карт бубновой масти), m_B = 4 ( в колоде 4 туза), n = 36 (число всех карт в колоде). Тогда P(A) = 9/39, P(B) = 4/36.

События А и В совместные (т.к. если будет извлечен бубновый туз, то произойдут оба события). Совместное появление этих событий имеет один благоприятный исход – появление бубнового туза, т.е.P(AB) = 1/36. Очевидно, что сумма А + В и есть событие, состоящее в появлении карты бубновой масти или туза. По теореме появления хотя бы одного из двух совместных событий имеем

P(A+B) = P(A) + P(B) – P(AB) = 9/36 + 4/36 – 1/36 = 12/36 = 1/3.

§5. Зависимые и независимые события. Условная вероятность.

Определение. Событие В называется независимым от события А, если вероятность события В не зависит от того, произошло событие А или нет. Событие В называется зависимым от события А, если вероятность события В меняется в зависимости от того, произошло событие А или нет.

Пример:

В первом ящике находится 4 красных и 6 белых шаров, во втором ящике – 5 красных и 4 белых шара. Из первого ящика во второй не глядя переложили один шар, после чего из второго извлекли один шар. Рассмотрим события

А – из первого ящика переложили белый шар;

В – из второго ящика извлекли белый шар.

Найдем вероятности событий A и B. Для события Авероятность равна 0,6 (почему?), а вот вероятность события В будет зависеть от того, произошло А или нет:

Если А произошло, то во втором ящике стало 10 шаров, из которых 5 белых, тогда

P(B) = 5/10 = 0,5; если же событие А не произошло (т.е. переложили не белый шар), то во втором ящике стало 10 шаров, из которых 4 белых и P(B) = 4/10 = 0,4. Таким образом, событие В зависит от события А, т.е. события А и В – зависимые.

Определение. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

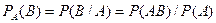
В предыдущем примере 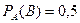а .

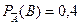§6. Вероятность произведения событий.

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

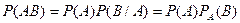
Также можно записать: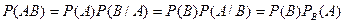

Доказательство этой теоремы непосредственно вытекает из определения условной вероятности.

Если события независимые, то 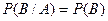, и теорема умножения вероятностей принимает вид:

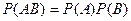
В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.

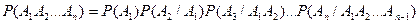
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.

Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

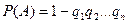
Здесь событие А обозначает наступление хотя бы одного из событий A_i, а q_i – вероятность противоположных событий .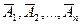

Пример 1. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.

Решение.

Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.

Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.

Всего в колоде 13 червонных и 13 бубновых карт.

Найдем вероятность события, противоположного событию С (среди извлеченных карт не будет ни бубновых ни червовых):

при вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна 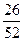, при вытаскивании второй карты - 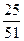, третьей - 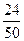, четвертой - .

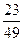Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна .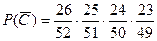

Искомая вероятность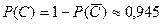

Пример 2. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?

Решение.

Вероятность выпадения 6 очков при одном броске кости равна . Вероятность того, что не выпадет 6 очков - 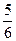. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна .

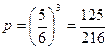Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна .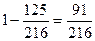

Пример 3. В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятности: а) хотя бы одного выстрела, б) двух выстрелов, в) двух осечек.

Решение.

Вероятность выстрела при первом нажатии на курок (событие А) равна 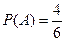, вероятность осечки - 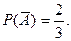Вероятность выстрела при втором нажатии на курок зависит от результата первого нажатия.

Так если в первом случае произошел выстрел, то в барабане осталось только 3 патрона, причем они распределены по 5 гнездам, т.к. при втором нажатии на курок напротив ствола не может оказаться гнездо, в котором был патрон при первом нажатии на курок.

Условная вероятность выстрела при второй попытке - 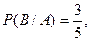если в первый раз был выстрел, 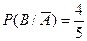- если в первый раз произошла осечка.

Условная вероятность осечки во второй раз - 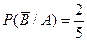, если в первый раз произошел выстрел, 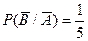- если в первый раз была осечка.

Рассмотрим вероятности того, что во втором случае произойдет выстрел (событие В) или произойдет осечка (событие 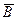) при условии, что в первом случае произошел выстрел (событие А) или осечка (событие ).

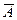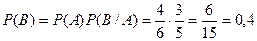- два выстрела подряд

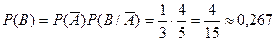- первая осечка, второй выстрел

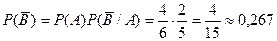- первый выстрел, вторая осечка

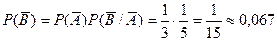- две осечки подряд

Эти четыре случая образуют полную группу событий (сумма их вероятностей равна единице)

Анализируя полученные результаты, видим, что вероятность хотя бы одного выстрела равна сумме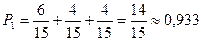

Пример 4. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Решение.

Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие 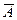, промах второго – событие .

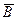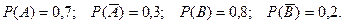
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна

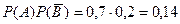
Вероятность того, что второй стрелок попадет в цель, а первый – нет равна

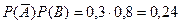
Тогда вероятность попадания в цель только одним стрелком равна

Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:

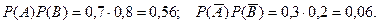
Тогда вероятность того, что в цель попадет только один стрелок равна:

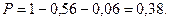
Пример 5. Вероятность того, что взятая наугад деталь из некоторой партии деталей, будет бракованной равна 0,2. Найти вероятность того, что из трех взятых деталей 2 окажется не бракованными.

Решение.

Обозначим бракованную деталь – событие А, не бракованную – событие .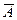

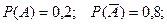
Если среди трех деталей оказывается только одна бракованная, то это возможно в одном из трех случаев: бракованная деталь будет первой, второй или третьей.

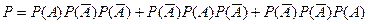
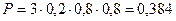
Пример 6. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.

Решение.

а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна

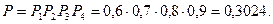
Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках.

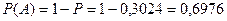б) Вероятность того, что нужная деталь находится не менее, чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность равна вероятности того, что деталь не находится только в одном ящике и имеется вообще.

123

Дата добавления: 2016-05-25; просмотров: 907;