Отображения многообразий
Пусть заданы два многообразия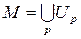 
, на котором введены координаты 
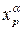, и 
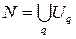с координатами 
.
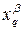Определение. Отображение f: M ® N называется гладким класса гладкости k, если функции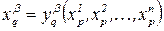 
для всех пар (p,q), когда они определены, в областях, где они определены, являются гладкими класса гладкости k.
Замечание 1. Не имеет смысла говорить о классе гладкости отображения более высоком, чем класс гладкости самих многообразий M и N.
Замечание 2. В случае, когда N – действительная прямая (N=R), отображение f:M®Rназывается числовой функцией f(x) на многообразии M (xÎM).
Можно дать более привычное определение гладкого отображения. Для этого нам понадобятся следующие вспомогательные понятия и определения.
Рассмотрим пространство Rn – пространство упорядоченных наборов x=(x1,x2,…,xn), составленных из действительных чисел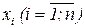 
, которые называются точками или векторами. Будем считать, что Rn стандартно вложено в Rn+k, т.е. точку (x1,x2,…,xn)ÎRn будем отождествлять с точкой (x1,x2,…,xn,0,…,0)ÎRn+k. Числа x1, x2,…, xn называются стандартными координатами точки x.
Пусть UÌRn – открытое множество. Всякое отображение f:U®Rm можно представить как упорядоченный набор функций:
f(x1,x2,…,xn)=(f1(x1,x2,…,xn), f2(x1,x2,…,xn),…, fn(x1,x2,…,xn)).
Определение. Отображение f:U®Rm называется гладким или дифференцируемым класса гладкости k, k³1 на U, если каждая функция fi(x1,x2,…,xn)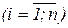 
имеет все непрерывные частные производные на U до k порядка включительно.
Гладкие отображения f класса k называются также Ck–отображениями и обозначаются fÎCk.
Если все функции fi имеют непрерывные частные производные любого порядка, то отображение, то отображение называется бесконечно гладким и обозначается C¥. Непрерывное отображение называется C0–отображением. Справедливы следующие включения
C¥Ì…ÌCkÌ…ÌC2ÌC1ÌC0.
Определение. Ck–пространство называется Ck–многообразием или многообразием класса Ck, если оно является топологическим многообразием (т.е. хаусдорфово и имеет счетную базу).
Многообразия класса Ck при k³1 называются гладкими или дифференцируемыми, а многообразия класса C¥ – аналитическими.
Определение. Два многообразия M и N называются гладко эквивалентными (диффеоморфными), если найдется взаимно однозначное и гладкое в обе стороны отображение f класса гладкости k³1:
f: M®N и f-1: N®M.
Замечание. Если два многообразия диффеоморфны, то якобиан преобразования локальных координат
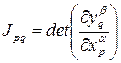
всюду отличен от нуля во всех тех областях, где функции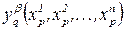 
определены.
Диффеоморфизм многообразий является отношением эквивалентности.
Следующие свойства диффеоморфизма вытекают из теорем дифференциального исчисления.
1. Если открытое подмножество пространства Rp или полупространства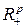 
диффеоморфно открытому подмножеству пространства Rn или полупространства 
, то n=p.
2. Открытое подмножество полупространства , диффеоморфное открытому подмножеству пространства Rn, открыто в Rn.
3. Диффеоморфизм, обратный диффеоморфизму класса Ck, принадлежит классу Ck.
Очевидно, что тождественное отображение Ck–пространства есть Ck–диффеоморфизм.
4. Композиция двух Ck-диффеоморфизмов есть Ck-диффеоморфизм.
Дата добавления: 2016-06-02; просмотров: 851;