Сепарабельность, компактность, связность.

Определение. Топологическое пространство называется сепарабельным, если оно содержит хотя бы одно счетное всюду плотное множество, т.е. такое множество, замыкание которого совпадает со всем топологическим пространством.

Определение. Топологическое пространство называется компактным, если любое его открытое покрытие содержит конечное подпокрытие.

Определение. Топологическое пространство называется локально компактным, если любая его точка имеет компактную окрестность.

Примеры: 1.Евклидово пространство Eⁿ не компактно, но локально компактно.

2.Сфера в Eⁿ компактна.

Теорема 1. Топологическое пространство со счетной базой сепарабельно.

Теорема 2. Для любого Т₁-пространства (X,t) следующие условия равносильны:

1. (X,t) регулярно и имеет счетную базу;

2. (X, t) метризуемо и сепарабельно;

Теорема Гейне – Бореля - Лебега. Каждое открытое покрытие произвольного замкнутого ограниченного подмножества пространства вещественных чисел является компактным подпространством.

Следствие. Замкнутое ограниченное подмножество n-мерного евклидова пространства компактно.

Определение. Два множества A и B в топологическом пространстве (X,t) называются отделенными, если 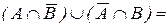Æ.

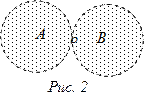
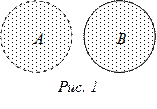
Примеры: 1. На следующих рисунках множества A и B отделены.

2. В естественной топологии числовой прямой отрезки [2,4] и [5,6] отделены, интервалы (1,2) и (2,3) отделены, множества (1,3) и [3,4) не отделены.

Определение. Топологическое пространство называется связным, если его невозможно представить в виде объединения двух непустых отделенных подмножеств.

Теорема 4. Пространство связно тогда и только тогда, когда оно содержит только тривиальные открыто-замкнутые множества.

Примеры: 1. Антидискретное пространство связно.

2. Дискетное пространство, содержащее более чем одну точку, несвязно.

3.Отрезок [0;1] числовой прямой – связное топологическое пространство, интервал (0;1) связен, числовая прямая связна.