Свойства перспективного отображения.

1. Перспективное отображение биективно;

2. Общая точка прямых при перспективном отображении переходит в себя;

3. При перспективном отображении сохраняется двойное или сложное отношение четырех точек

Теорема 5.8. (Паскаля – Паппа).

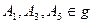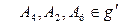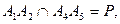
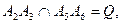
Пусть на различных прямых взяты по три различных точки и . Точки пересечения прямых 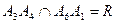лежат на одной прямой.

Доказательство.

1.Рассмотрим проективное отображение 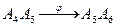. Определим это проективное отображение как композицию двух перспективных отображений

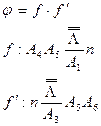
2. Введем дополнительные точки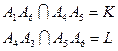

3. Рассмотрим образы точек прямой А₄А₅ при двух перспективных отображениях

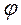
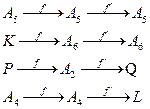
Проективное отображение 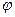, переводящее А₄А₅ в А₅А₆, переводит точку А₅ в себя, а значит 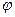- перспективное отображение по свойству 3.

4. Найдем центр перспективы. Так как 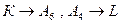, то центр перспективы совпадает с точкой пересечения прямых .

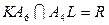5. Точка 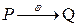, следовательно PQ проходит через R, а значит, P,Q,R коллинеарны.

Определение 5.9. Взаимное отображение пучка 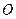на пучок 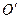называется проективным, если оно сохраняет сложное отношение четырех прямых.

Теорема 5.10.Существует единственное отображение, переводящее пучка 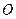в пучок 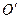, переводящее прямые 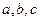пучка 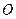в прямые 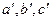пучка .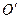

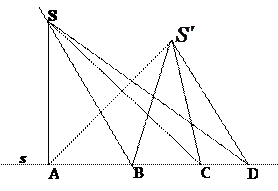Определение 5.11.Два пучка и называются перспективными, если они перспективны одному и тому же прямолинейному ряду (прямой), или иначе, если они проектируют один и тот же ряд, следовательно, все точки пересечения соответственных прямых пучков и 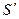лежат на одной прямой 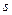, называемой осью перспективы.