Проективные отображения прямых и пучков.

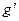Пусть даны две произвольные прямые и на проективной плоскости.

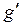Определение 5.4. Взаимно однозначное отображение множества точек прямой на множество точек называется проективным отображением, если сохраняется сложное отношение четырех точек .

Теорема 5.5. Если на различных прямых и 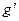заданы соответственно реперы , то существует единственное проективное отображение, переводящее репер R в репер .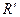

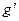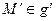Определение 5.6. Проективное отображение прямых и , при котором произвольная точка переходит в точку ,так что точки 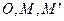коллинеарны, где 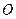- произвольная точка проективной плоскости, отличная от 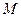и 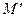и не принадлежащая данным прямым, называется перспективным отображением с центром в точке О.

Обозначение перспективного отображения: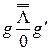

Два прямолинейных ряда 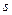и называются перспективными, если они перспективны одному и тому же пучку, или иначе, если они являются сечениями одного и того же пучка, т.е. все прямые, соединяющие соответственные точки рядов 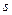и , пересекаются в одной точке 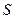(согласно рисунку точке О).

Лемма 5.7. Любое проективное отображение одной прямой на другую может быть разложено в композицию не более двух перспективных отображений, если прямые и 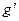различны, и не более трех перспективных отображений, если прямые и 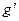совпадают.