Построение четвёртой гармонической точки к трем данным
Свойства полного четырехвершинника.
1. На каждой стороне полного четырехвершинника имеется гармоническая четверка точек: одна пара точек этой четверки – вершины, другая образована диагональной точкой и точкой пересечения этой стороны с диагональю, проходящей через две другие диагональные точки.
2. На каждой диагонали полного четырехвершинника имеется гармоническая четверка точек: одна пара точек этой четверки – диагональные точки, другая – точки пересечения сторон, проходящих через третью диагональную точку, с данной диагональю.
3. Через каждую диагональную точку полного четырехвершинника проходит гармоническая четверка прямых: одна пара прямых – две противоположные стороны, другая – две диагонали.
В силу свойств полного четырехвершинника построение четвертого гармонического элемента может быть выполнено проективными средствами, т.е. с помощью одной линейки.
Построение четвёртой гармонической точки к трем данным
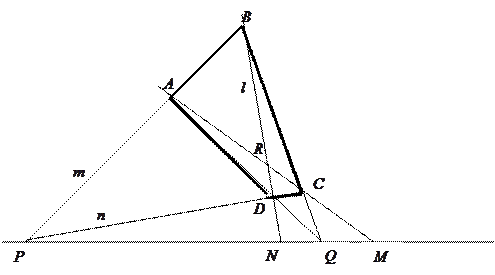 |
Задача №1. Пусть дана прямая
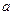 и различные точки
и различные точки 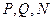 . Построить точку
. Построить точку 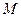 прямой
прямой 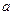 , такую, что
, такую, что 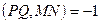
Решение.
1. Проводим через точку 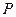 две произвольные прямые
две произвольные прямые 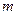 и
и 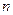 .
.
2. Через точку 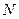 проводим произвольную прямую
проводим произвольную прямую 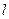 :
:  .
.
3. Проводим прямые 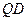 и
и 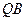 :
: 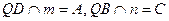 .
.
4. Проводим прямую 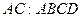 - полный четырехвершинник.
- полный четырехвершинник.
5. По свойству 2 точка пересечения 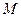 стороны
стороны  с диагональю
с диагональю 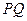 является четвертой гармонической к точкам
является четвертой гармонической к точкам 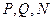 .
.
Задача №2. Построить четвертую гармоническую точку 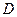 к трем данным точкам
к трем данным точкам  на расширенной прямой.
на расширенной прямой.
Решение.
1. Возьмем на расширенной прямой репер 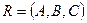 . Пусть точка
. Пусть точка 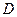 имеет координаты
имеет координаты 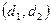 относительно данного репера. По свойству сложного отношения четырех точек имеем:
относительно данного репера. По свойству сложного отношения четырех точек имеем:  и значит
и значит 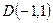 .
.
2. Построим точку 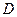 по координатам относительно данного репера.
по координатам относительно данного репера.
Дата добавления: 2017-01-29; просмотров: 4105;
