Определение топологического пространства

Определение. Покрытием множества A называется такое семейство множеств {U_a}, что объединение элементов этого семейства содержит множество A: .

Замечание. В общем случае элементы покрытия могут как содержаться в покрываемом множестве, так и содержать элементы, не принадлежащие ему.

Примеры:

1.Черепица на крыше является покрытием крыши, если она не течет.

2.Если A=R, то следующие семейства являются его покрытиями:

а) {U_a}={(n-1;n+1), nÎZ};

б) {U_a}={[n-1;n], nÎZ};

в) {U_a} – множество всех открытых интервалов. Забегая вперед, скажем, что это покрытие образует топологию числовой прямой, которая называется естественной.

3.Множество кругов на плоскости является покрытием плоскости, а также любой фигуры, лежащей в этой плоскости.

Определение. Подпокрытием покрытия {U_a} множества A называется такое подсемейство {U_b}Ì{U_a}, которое само является покрытием множества A.

Примеры. 1.В случае примеров 1, 2а, 2б подпокрытий нет.

2.Если из множества всех открытых интервалов (пример 2в) выделить, например, семейство 2а, то это будет подпокрытие.

3.Семейство {U_b}={{a,b,m}, {b,c,m}, {c,d,m}, {a,k,m}} является покрытием множества A={a,b,c,d,k}, причем элементы покрытия не содержатся в A; покрытие {U_b} подпокрытий не содержит.

Определение. Топологией t на множестве X называется такое покрытие этого множества, элементы которого являются подмножествами X и удовлетворяют следующим аксиомам:

1) ÆÎt (пустое множество является элементом из t);

2) XÎt (множество X - элемент из t);

3) 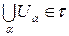(объединение любого числа элементов из t - элемент из t);

4) 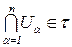(пересечение конечного числа элементов из t - элемент из t).

Определение. Топологическим пространством называется пара (X, t), где X – непустое множество с некоторой топологией t.

Определение. Элементы любой топологии называются открытыми множествами этой топологии, а элементы пространства X называются точками топологии.

С учетом данного определения аксиомы топологического пространства могут быть сформулированы следующим образом:

1) Æ открыто;

2) множество X открыто;

3) объединение любого числа открытых множеств открыто;

4) пересечение конечного числа открытых множеств открыто.

Примеры: 1.На любом множестве X≠Æ всегда существует топология, называемая тривиальной или антидискретной, состоящая из самого множества X и Æ. Антидискретная топология является минимальной топологией на X.

2.В пространстве Rⁿ множество открытых параллелепипедов задает топологическое пространство с естественной топологией.

Определение. Множество A называется замкнутым в топологическом пространстве (X, t), если его дополнение C_XA до множества X открыто в топологии этого пространства.

Замечание. Достаточно очевидно, что произвольное множество в топологическом пространстве может быть открытым, замкнутым, открыто-замкнутым и не открытым и не замкнутым. В частности, множества Æ и t являются открыто-замкнутыми в любой топологии и в силу этого называются тривиальными открыто-замкнутыми множествами.

Пример. Пусть X - произвольное непустое множество, а t - множество всех подмножеств множества X. Тогда t - топология на X. Эта топология называетсядискретной. Она является максимальной топологией на X. Характерным для дискретной топологии является то, что в этой топологии любое подмножество открыто - замкнуто.

§2 Взаимное расположение точек и множеств