РОБОТА РОЗШИРЕННЯ ПРИ РІЗНИХ ПРОЦЕСАХ

Розглянемо роботу рассширения, чинену одним молем ідеального газу, у різних умовах:

1) Ізотермічний процес (T = const). Оскільки внутрішня енергія ідеального газу залежить тільки від температури й не залежить від об'єму (закон Джоуля)

U = const Þ dU = 0, (7)

тоді

dQ – dA = 0 Þ dQ = dA = 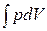. (8)

Скористаємося рівнянням стану ідеального газу:

p = RT Þ p = 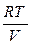, (9)

тоді

Q_T = A_T = 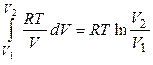. (10)

Таким чином, робота оборотного ізотермічного розширення ідеального газу відбувається тільки за рахунок підведеної теплоти.

2) Ізохорний процес (V = const). Отже

A_V = 0. (11)

Тоді

dQ_V = d,(12)

Q_V = ∆U. (13)

Вся теплота, підведена до системи, іде на збільшення внутрішньої енергії. Таким чином, Q_V є мірою зміни внутрішньої енергії (в ізохорному процесі робота розширення не відбувається).

3) Ізобарний процес (p = const). Відповідно до першого закону

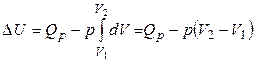, (14)

або

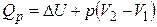, (15)

т. ч. не вся теплота, підведена до системи, іде на збільшення внутрішньої енергії. Частина її витрачається на роботу розширення.

Останнє вираження можна записати в наступному виді:

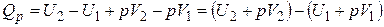. (16)

Уведемо нову функцію стану — ентальпію:

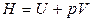. (17)

Отже,

, (18)

т. е. теплота теплота ізобарного процесу дорівнює зміні ентальпії.

Зміна ентальпії як функції стану не залежить від шляху протікання процесу, і є корисною величиною при аналізі різних термодинамічних процесів.

Для хімічних реакцій у газовій фазі справедливо:

Q_P – Q_V = ∆(pV) = ∆nRT, (19)

т. е.

∆H = ∆U + ∆nRT, (20)

де ∆n — зміна числа моль газоподібних речовин у ході реакції.

Отже, ∆U відповідає тепловому ефекту ізохорного процесу, а ∆H – ізобарного.

ЗАКОН ГЕССА.

В 1836 році російським академіком Г. И. Гессом встановлено досвідченим шляхом, що тепловий ефект хімічної реакції не залежить від шляху її протікання, а визначається лише початковим і кінцевим станом системи при p = const або V = const.

Закон Гесса дає можливість розрахувати теплові ефекти процесів у тих випадках, коли їх важко виміряти в певних умовах або коли в цих умовах не можна здійснити цей процес.

Тепловий ефект реакції – максимальна кількість теплоти, що виділяється в необоротному процесі при p = const або V = const, якщо всі речовини мають однакову температуру й відсутні інші види робіт, крім роботи розширення.

У хімічній термодинаміці стандартним станом називається стан системи, обиране як крапка відліку при оцінці термодинамічних величин. Необхідність вибору стандартного стану обумовлена тим, що в рамках хімічної термодинаміки не можуть бути розраховані абсолютні значення енергій Гіббса, ентальпій і інших термодинамічних функцій для даної речовини. Стандартний стан характеризується стандартними умовами – температура 25°С (298 К) і тиск 1 атм. Теплові ефекти, віднесені до цих умов, називаються стандартними тепловими ефектами.

Як стандартний стан для простих речовин приймають стійкий фазовий і хімічний стан елемента при даній температурі.

Для розрахунку теплового ефекту хімічних реакцій використовують термохімічні рівняння, у яких обов'язково вказується агрегатний стан реагуючих речовин і продуктів реакції; для твердих речовин вказується їхня поліморфна модифікація: С_графит, С_алмаз. У термохімічному рівнянні також вказується тепловий ефект реакції або зміна ентальпії хімічної реакції, розрахованої для стандартних умов.

Основу всіх термохімічних розрахунків становить закон Гесса, який можна представити у вигляді:

Q_V = ∆U, V = const, (21)

Q_P = ∆H, p = const.(22)

Наслідки із закону Гесса:

Наслідок 1. Тепловий ефект реакції дорівнює різниці сум теплот утворення продуктів реакції й сум теплот утворення вихідних речовин при стандартних умовах, помножених на відповідні стехиометрические коефіцієнти.

, (23)

знак «^o» означає стандартні умови, f – “formation” (утворення).

Стандартна теплота утворення речовини – це теплота реакції утворення речовини із простих речовин, стійких за даних умов.

Наслідок 2. Тепловий ефект реакції при стандартних умовах дорівнює різниці між сумою теплот згоряння вихідних речовин і сумою теплот згоряння продуктів реакції, помножених на відповідні стехіометричні коефіцієнти.

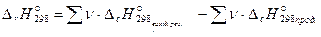(24)

Стандартна теплота згоряння – теплота, що виділяється при згорянні в атмосфері кисню 1 молячи речовини при стандартних умовах до вищих оксидів. Причому, всі учасники реакції повинні бути в стійких агрегатних станах.

У хімічній термодинаміці найчастіше розглядаються ізобарні процеси (p = const), для яких Q_P = ∆H. Тому термін «тепловий ефект реакції» заміняють терміном «ентальпія реакції». Ентальпія реакції – це зміна ентальпії системи при протіканні хімічної реакції. Вона може бути більше нуля або менше нуля.

Якщо ∆H > 0, то Q > 0 (ендотермічні реакції).

Якщо ∆H < 0, то Q < 0 (екзотермічні реакції).

Наслідок 3. Тепловий ефект розкладу хімічної сполуки дорівнює за абсолютною величиною і протилежний за знаком тепловому ефекту утворення цієї сполуки (закон Лавуаз’є-Лапласа):

Hpозкл = – Нутв

Наприклад, ½Н₂ + ½І₂ = НІ ∆Н₁ = – 26,6 кДж;

НІ = ½Н₂ + ½І₂ ∆Н₂ = 26,6 кДж.

Наслідок 4. Якщо здійснюються дві реакції, що приводять із різних початкових до однакових кінцевих станів, то різниця між їх тепловими ефектами являє собою тепловий ефект переходу з одного початкового стану в інший. Це дозволяє обчислювати процеси, які ми не маємо можливості практично здійснити.

Наприклад, перетворення графіту в алмаз:

C(графіт) + О₂(г) = СО₂ ∆Н₁ = – 393,5 кДж

C(алмаз) + О₂(г) = СО₂ ∆Н₂ = – 395,33 кДж

C(графіт) → C(алмаз) ∆Н₁ – ∆Н₂ = 1,83 кДж

Наслідок 5. Якщо відбуваються дві реакції, які приводять із однакових початкових до різних кінцевих станів, різниця між їх тепловими ефектами являє собою тепловий ефект переходу з одного кінцевого стану в інший.

Термохімічні рівняння можна додавати (віднімати) одне до одного разом з їх тепловими ефектами, як алгебраїчні рівняння.

Для оборотних хімічних реакцій ентальпії прямої ( 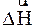) і зворотної ( 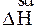) реакцій рівноцінні між собою, але мають протилежні знаки, тобто, якщо пряма реакція є екзотермічною ( 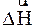< 0), то це означає, що зворотна реакція буде ендотермічною ( 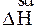> 0) за умови, що числові їх значення однакові = .

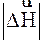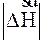Закон Гесса поширюється не тільки на різноманітні хімічні реакції, а й на фізико-хімічні процеси, які супроводжуються енергетичними ефектами, такими як: фазові перетворення (плавлення, випаровування, конденсація, кристалізація), розчинення. У випадку оборотних фізико-хімічних процесів, так званих міжфазових переходів, ентальпії прямих і зворотних процесів чисельно рівні між собою, але протилежні за знаком, що можна продемонструвати такою схемою:

,

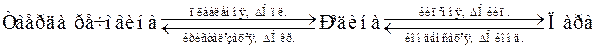
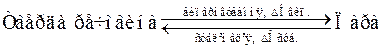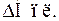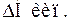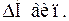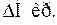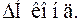причому > 0, > 0, > 0, тоді як < 0, < 0, < 0.

ТЕПЛОЄМНІСТЬ.

Теплоємність– це кількість теплоти, який необхідно повідомити або відняти тілу або системі, щоб їхня температура змінилася на 1 градус. Теплоємність — величина екстенсивна, тому що залежить від розміру системи. Теплоємність,розрахована на 1 моль речовини, називається мольної, а на одиницю маси – питомої.

Розрізняють:

— істина теплоємність: [ 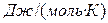], де 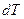– нескінченно мала зміна температури. (25)

— середню теплоємність – відношення кількості теплоти, якої було надано системі, до відповідної зміни температури: 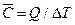(26)

Теплоємність не є функцією стану, оскільки її значення визначається кількістю теплоти, що залежить від характеру процесу.

Найбільше часто використовуються наступні теплоємності:

1. Ізохорна теплоємність. При нагріванні або охолодженні речовини при постійному об'ємі справедливо:

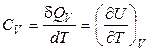. (27)

2. Ізобарна теплоємність. При нагріванні або охолодженні речовини при постійному тиску справедливо:

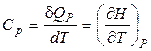. . (28)

Теплоємність при постійному тиску С_р більше, ніж теплоємність при постійному об'ємі С_V, тому що нагрівання речовини при постійному тиску супроводжується роботою розширення, тобто

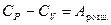. (29)

Для ідеальних газів справедливе рівняння Майєра:

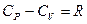* (30)

Величина R (універсальна газова постійна) дорівнює роботі розширення 1 моля ідеального газу (при р = const) при збільшенні його температури на 1 градус.

Відношення 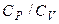позначається символом 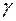(адіабатичний коефіцієнт), що завжди більше нуля ( 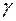> 0).

*Якщо нагрівають газ, то згідно з першим законом термодинаміки:

,

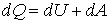а для одного моля газу:

.

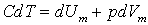Якщо газ нагрівається при сталому об'ємі, то надана газу теплота йде лише на збільшення його внутрішньої енергії:

.

Якщо газ нагрівається при постійному тиску, то:

.

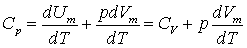Тут враховано, що 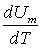не залежить від виду процесу, оскільки внутрішня енергія ідеального газу не залежить ні від 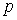, ні від 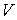, а визначається лише температурою. Тому завжди .

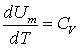Згідно з рівнянням Менделєєва-Клапейрона:

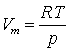і .

В результаті:

.

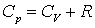Розглядаючи теплоємність одно-, двох- і трьохатомних ідеальних газів, використовують поняття «кількість ступенів вільності (свободи) – і». Кількістю ступенів вільності називається кількість незалежних видів руху, на які можна розкласти даний вид руху, або кількість координат, необхідна для визначення положення молекули в просторі. Таким чином, одноатомна молекула має 3 поступальні ступені вільності, двохатомна молекула має 5 ступенів (3 поступальні і 2 обертальні), а багатоатомна молекула – 6 ступенів вільності (3 поступальні і 3 обертальні).

У класичній статистичній фізиці виводиться теорема про рівномірний розподіл енергії за ступенями вільності: якщо система молекул знаходиться в тепловій рівновазі при температурі T, то середня кінетична енергія рівномірно розподілена між усіма ступенями вільності і для кожного ступеня вільності молекули вона дорівнює З цієї теореми випливає, що молярні теплоємності газу C_p і C_V, які зв’язані рівнянням Майора і їх відношення γ можуть бути записані у вигляді:

Для газу, який складається з одноатомних молекул (i = 3)

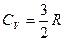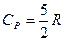; ; γ=1,66

Для газу, який складається з двохатомних молекул (i=5)

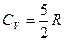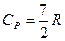; ; γ=1,4

Трьохатомні ідеальні гази з нелінійною структурою мають i=6

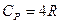; ; γ=1,33

У наведених розрахунках теплоємностей не бралися до уваги коливальні рухи атомів і атомних груп, а також електронні переходи, які не піддаються такому простому розрахунку. Оскільки енергії цих рухів зростають помітно тільки при дуже високих температурах (1000 – 2000 К), то всі наведені розрахунки справджуються для не дуже високих температур. При високих температурах цими рухами нехтувати не можна.

Теплоємність реальних газів при ускладненні їхніх молекул збільшується зі зростанням температури внаслідок появи поряд з поступальними та обертальними формами руху коливальних видів руху, а також через порушення принципу рівномірного розподілу енергії за ступенями вільності. І тому розрахувати теоретичне значення теплоємності реальних газів неможливо.

Залежність теплоємності речовин від температури зручно апроксимувати рівняннями:

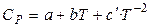для неорганічних речовин (31)

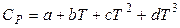для органічних речовин (32)

Значення a, b, c, c´, d наведені в довідниках фізико-хімічних і термодинамічних величин.