ДРУГИЙ ЗАКОН ТЕРМОДИНАМІКИ. ЕНТРОПІЯ.

Всі процеси, що протікає в природі, підкоряються першому закону термодинаміки, однак не всякий можливий процес здійснимо на практиці. Виходячи з першого закону, не можна вирішити, чи відбувається мимовільно перехід теплоти від нагрітого тіла до холодного або навпаки, тобто не можна визначити напрямок мимовільного процесу (процесу, що відбуває спонтанно без зовнішніх впливів).

Другий закон термодинаміки дозволяє визначити напрямок процесу при заданих умовах. На відміну від першого закону термодинаміки він не носить загального характеру, і застосуємо лише до систем, що складають із великої кількості часток.

Відкриттю другого закону термодинаміки передував винахід теплових машин – пристроїв, які можуть перетворювати теплоту в роботу. Природність хаотичного руху молекул приводить до того, що теплоту не можна повністю перетворити в роботу. А роботу можна повністю перетворити в теплоту - це принципова відмінність теплоти від роботи.

Будь-який хімічний процес можна представити як сукупність двох явищ: по-перше, передачі енергії, по-друге, зміна впорядкованості у взаємному розташуванні часток. Якісно охарактеризувати розсіювання теплової енергії покликана ентропія, що позначається символом S. Ентропія - міра невпорядкованості системи. При переході системи з більше впорядкованого стану в менш упорядкований стан ентропія системи зростає, а при переході системи з менш упорядкованого в більше впорядкований стан ентропія системи зменшується.

Існує кілька формулювань другого закону термодинаміки:

1. Формулювання по Клаузиусу. Теплота не може мимовільно переходити від більше холодного тіла до більше гарячого.

2. Формулювання по Оствальду. Вічний двигун другого роду неможливий (тобто не існує машини, яка б повністю перетворювала теплоту в роботу, частина теплоти має віддаватися холодильнику).

3. Формулювання по Томсону. Неможливо одержувати роботу при наявності тільки одного джерела тепла в циклічно діючій машині.

У теплових машинах речовина (робоче тіло) робить цикл процесів, вертаючись в початковий стан. Найпростішим прикладом є цикл Карно (робоче тіло – ідеальний газ), що складається із двох ізотерм і двох адіабат. Використовуючи цикл Карно, можна довести, що наведена теплота Q/T має властивості функції стану. Ентропія також є функцією стану (тому що число способів, якими можна реалізувати той або інший стан, не залежить від шляху переходу в нього) і її зміна в будь-якому рівноважному (оборотному) процесі дорівнює наведеній теплоті:

, (1)

або

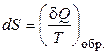. (2)

Варто враховувати, що для необоротних процесів наведена теплота не є функцією стану й

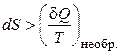. (3)

Отже, другий закон термодинаміки: в ізольованій системі мимовільно протікають тільки такі процеси, які ведуть до збільшення невпорядкованості системи, тобто до росту ентропії. Основний зміст цього закону полягає в тому, що в будь-якій ізольованій системі із часом відбувається постійне зростання ступеня безладдя, а, виходить, і ріст ентропії.

Ентропія – це екстенсивна функція стану системи, диференціал якої при термодинамічно оборотному процесі дорівнює відношенню нескінченно малої кількості теплоти, наданої системі, до температури системи, а при термодинамічно необоротному процесі більша за це відношення.

У загальному вигляді аналітичний вираз другого закону термодинаміки має такий вигляд:

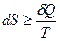. Знак «>» відповідає термодинамічно необоротним процесам, знак «=» – термодинамічно оборотним процесам.

За визначенням в ізольованій системі можуть відбуватися тільки самочинні процеси. Характеристики існування ізольованої системи:

U=const, dU=0;

V=const, δA=PdV=0.

Тоді перший закон термодинаміки для ізольованої системи набирає такого вигляду:

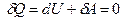. Тобто для ізольованої системи .

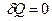Згідно з другим законом термодинаміки 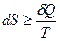. Тоді для ізольованої системи виконується така умова 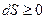– математичний вираз другого закону термодинаміки для ізольованої системи.

В ізольованій системі зміна ентропії служить критерієм напрямку процесу, тобто є критерієм оборотності й необоротності процесів: якщо в процесі d S> 0, то він мимовільний, необоротний, а якщо dS = 0, то він рівноважний, оборотний. Ентропія ізольованої системи або збільшується, або залишається постійної, і в стані рівноваги ентропія максимальна: S_u,v = S_max і (∆S)_u,v = 0.

Слід зазначити, що якщо процес протікає в неізольованій системі, то для оцінки необоротності процесу необхідно мати величину зміни ентропії системи й величину зміни ентропії навколишнього середовища.