Нелинейная регрессия

НЕКОТОРЫЕ ВОПРОСЫ СПЕЦИФИКАЦИИ

РЕГРЕССИОННЫХ МОДЕЛЕЙ

К основным вопросам спецификации модели традиционно относят два типа задач.

Первый – это выбор структуры уравнения регрессии, т. е. математической формы модели.

Второй – это определение качественного и количественного состава объясняющих переменных (факторов-аргументов). Неправильные постановка и решение этих задач приводят к появлению в создаваемых моделях ошибок спецификации.

Можно заметить, что при проведении эконометрического анализа приходится постоянно сталкиваться с вопросами спецификации модели, например, при определении значимости регрессоров, при рассмотрении мультиколлинеарности и т. д. В целом работоспособной является модель с правильной спецификацией. Это означает, что уравнение регрессии достаточно надежно определяет соотношение между исследуемыми экономическими показателями.

В данной главе рассмотрены наиболее общие вопросы спецификации, позволяющие учитывать реальные ситуации, возникающие при эконометрическом моделировании.

Нелинейная регрессия

В силу многообразия и сложности экономических процессов невозможно ограничиться рассмотрением лишь линейных регрессионных моделей, т. к. многие экономические зависимости являются нелинейными по своей сути. Например, при анализе зависимости общих издержек от объема выпуска наиболее обоснованной является полиномиальная модель. При рассмотрении производственных функций обычно используются модели, содержащие показательные функции (например, широко известная в экономике функция Кобба-Дугласа).

Мы ограничимся рассмотрением нелинейных моделей, допускающих их сведение к линейным путем преобразования переменных. В рамках этого подхода для линеаризации могут быть использованы модели как нелинейные по переменным, так и нелинейные по параметрам.

Наиболее просто осуществляется линеаризация, если модель нелинейна по переменным. В этом случае введением новых переменных модель можно свести к линейной, для оценки параметров которой используется обычный метод наименьших квадратов.

Рассмотрим некоторые примеры моделей, линейных по параметрам. Кубическая функция вида

(4.1)

в микроэкономике моделирует зависимость общих издержек (U) от объема выпуска (Q) (рис. 4.1а).

Аналогично квадратичная функция

(4.2)

может отражать зависимость между объемом выпуска (Q) и средними ( ) издержками (рис. 4.1б); или расходами на рекламу (С) и прибылью (П) (рис. 4.1в).

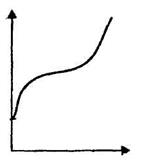
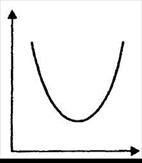
а б в

Рис. 4.1.

Заменяя Х на Х₁, Х² на Х₂, Х³ на Х₃, получаем вместо (4.1) и (4.2) модели множественной линейной регрессии, где исходные факторные данные необходимо представлять в соответствующих степенях.

Модель вида

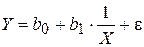(4.3)

называется обратной моделью. Эта модель сводится к линейной парной регрессии заменой 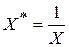. Подобные модели обычно применяются в тех случаях, когда неограниченное увеличение объясняющей (факторной) переменной Х асимптотически приближает зависимую переменную Y к некоторому пределу (в данном случае к b₀). Например, данная модель может отражать зависимость между доходом Х и спросом на определенные товары Y (рис. 4.2).

Рис. 4.2.

Более сложной проблемой является нелинейность модели по параметрам, т. к. в данном случае при применении МНК к линеаризованным моделям необходимо учитывать результаты преобразования случайного отклонения e. К числу таких моделей можно отнести, например, мультипликативную (степенную) модель

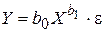(4.4)

и экспоненциальную модель

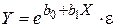. (4.5)

Подобные модели могут быть сведены к линейным логарифмированием обеих частей уравнений. Тогда, например, модель (4.4) примет вид

lnY = lnb₀ + b₁lnX + lne. (4.6)

Полученное уравнение является линейным относительно логарифмов переменных, т. е. модель может быть оценена и проанализирована обычными методами линейного регрессионного анализа. Однако следует заметить, что для эффективного применения МНК в данной модели случайное отклонение e должно иметь логарифмически нормальное распределение.

Приведенная модель (4.6) называется логарифмической и легко обобщается на большее число переменных.

В качестве примера использования линеаризирующего преобразования рассмотрим регрессионную модель на основе производственной функции Кобба-Дугласа

Y = AK^aL^β, (4.7)

где Y – объем производства; K – затраты капитала; L – затраты труда; A, a и β – параметры модели.

Показатели a и β являются коэффициентами частной эластичности объема производства по затратам капитала и труда соответственно. Это означает, что при увеличении одних только затрат капитала (труда) на 1 % объем производства увеличивается на a %( β %). Сумма этих коэффициентов является таким важным экономическим показателем, как отдача от масштаба производства. При a + β = 1 говорят о постоянной отдаче от масштаба (во сколько раз увеличиваются затраты ресурсов, во столько же раз увеличивается объем производства). При a + β < 1 имеет место убывающая отдача от масштаба (увеличение объема производства меньше увеличения затрат). В случае a + β > 1 наблюдается возрастающая отдача от масштаба (увеличение объема производства больше увеличения затрат ресурсов).

Учитывая возможное влияние неучтенных и случайных факторов, добавим в модель (4.7) случайное отклонение:

Y = AK^aL^βe. (4.8)

Полученную мультипликативную модель легко свести к линейной путем логарифмирования. Тогда, прологарифмировав (4.8), для конкретного i-го наблюдения имеем:

lny_i = lnA + alnK_i + βlnL_i + lne_i, i = 1, …, n. (4.9)

Если производственная ситуация соответствует постоянной отдаче от масштаба (a + β = 1), то модель на основе функции Кобба-Дугласа представляется в виде:

Y = AK^aL^{1 - a}e,

или (4.10)

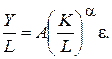
Таким образом, получаем зависимость производительности труда (Y/L) от его капиталовооруженности (K/L). Для оценки параметров модели (4.10) приводим ее к линейной парной регрессии

ln(Y/L)_i = lnA + aln(K/L)_i + lne, i = 1, …, n. (4.11)

В эконометрическом анализе используется также производственная функция Кобба-Дугласа с учетом научно-технического прогресса:

Y = AK^aL^βе^qte, (4.12)

где t – время; q – параметр, характеризующий темп прироста объема производства благодаря техническому прогрессу. Модель (4.12) сводится к линейной регрессии аналогично модели (4.8).

Следует заметить, что модель вида

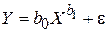(4.13)

отличается от (4.4) тем, что случайное отклонение здесь входит аддитивно, нельзя привести логарифмированием к линейному уравнению. В этом случае используются специальные итерационные процедуры оценивания параметров.

Пример 4.1. По данным, собранным по 20 предприятиям легкой промышленности (n = 20), оценить производственную функцию Кобба-Дугласа при постоянной отдаче от масштаба.

Рассмотрим функцию Кобба-Дугласа в виде (4.10). Исходные переменные модели K/L и Y/L. Логарифмируя и применяя к преобразованным данным МНК, получим*

,

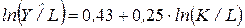стандартные ошибки (0,15) (0,04)

или в виде .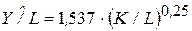

Коэффициент регрессии, равный 0,25, является также коэффициентом эластичности в рамках данной модели. Он показывает, что при увеличении капиталовооруженности труда на 1 % производительность труда на предприятиях отрасли увеличивается в среднем на 0,25 %.

Сравнивая наблюдаемое (расчетное) и табличное (критическое) значения t-статистики на уровне значимости a = 0,05, делаем вывод о том, что коэффициент регрессии, а значит и уравнение парной регрессионной модели, значимы.