Обобщенный метод наименьших квадратов

Одной из основных предпосылок получения «наилучших» оценок по МНК для классической регрессионной модели является предположение о том, что случайные отклонения (остатки) некоррелированы между собой и имеют постоянную дисперсию. В тех случаях, когда наблюдаемые объекты достаточно однородны или исследуемые в различные моменты времени экономические показатели оказывают незначительное влияние друг на друга, такое допущение вполне оправдано. Однако на практике нередко возникают экономические ситуации, когда данное условие является неприемлемым. Например, при исследовании зависимости потребления от дохода вполне реалистично считать, что с ростом дохода растет среднее значение потребления. Кроме того, следует ожидать, что разброс в потреблении будет более существенным для субъектов с большим уровнем дохода, так как люди с большим доходом имеют больший простор для его распределения. Это означает, что дисперсия потребления не остается постоянной, а изменяется (увеличивается) с ростом дохода. Приведенный пример характеризует ситуацию, когда дисперсии зависимых величин, а, следовательно, и случайных отклонений не постоянны. Это явление в эконометрике называется гетероскедастичностью (в отличие от гомоскедастичности – постоянства дисперсии отклонений).

При анализе временных рядов мы в большинстве случаев сталкиваемся с ситуацией, когда наблюдаемые в данный момент значения исследуемой переменой статистически зависят от ее значений в предыдущие моменты времени, что означает наличие корреляции между случайными отклонениями. Поэтому наряду с классическими моделями возникает необходимость рассматривать регрессионные модели без предположения, что ковариационная матрица случайных отклонений (см. раздел 3.2) имеет вид:

V(e) = σ²E.

В этом случае применяется так называемая обобщенная линейная модель множественной регрессии, в которой переменные и параметры определены так же, как и в классической модели (раздел 3.2), и выполняется следующая система условий:

1. Матрица независимых переменных Х неслучайна (детерминирована) и имеет полный ранг.

2. М(e) = 0.

3. V(e) = W, где W – положительно определенная симметричная матрица.

Таким образом, обобщенная модель отличается от классической только условием 3, т. е. видом ковариационной матрицы: вместо V(e) = σ²E, где Е - единичная матрица n-го порядка для классической модели следует рассматривать матрицу V(e) = W для обобщенной. Это означает, что, в отличие от классической, в обобщенной модели ковариации и дисперсии случайных отклонений (остатков) могут быть произвольными. В этом заключается суть обобщения регрессионной модели.

Применение обычного МНК к обобщенной модели приводит к тому, что найденные оценки параметров не являются эффективными в смысле минимума ковариационной матрицы, и дисперсии оценок будут рассчитываться со смещением. Это означает, что мы рискуем получить оценку вектора В, существенно отличающуюся от истинных значений параметров, и сделать неверные выводы по модели.

Для получения эффективной оценки в случае обобщенной модели следует воспользоваться так называемым обобщенным методом наименьших квадратов (ОМНК).

Оценка вектора В по ОМНК определяется выражением

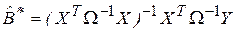(5.1)

и, согласно теореме Айткена, имеет наименьшую ковариационную матрицу в классе линейных несмещенных оценок для обобщенной регрессионной модели. В случае классической модели, т. е. при выполнении предпосылки V(e) = W = σ²E, оценка обобщенного метода наименьших квадратов 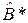совпадает с оценкой 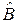обычного МНК.

Следует отметить, что для обобщенной модели коэффициент детерминации R² уже не является основной мерой качества построенной регрессии, а может использоваться лишь как приближенная (сравнительная) характеристика качества модели. В общем случае значения коэффициента детерминации могут выходить за пределы интервала [0, 1], а добавление или удаление регрессоров не обязательно приводит к его соответствующему увеличению или уменьшению.

Для оценки регрессионной модели с применением ОМНК по формуле (5.1) необходимо знать ковариационную матрицу остатков W, что в практике эконометрических исследований встречается крайне редко. Если же считать все n(n + 1)/2 элементов ковариационной матрицы неизвестными параметрами обобщенной модели (в дополнение к (m + 1) параметрам b_j), то общее число параметров всегда будет превосходить объем выборочных данных, что делает оценку параметров неразрешимой статистической задачей. Таким образом, существует проблема практической реализации ОМНК, которая может быть решена путем рассмотрения определенных дополнительных условий (априорных ограничений), накладываемых на структуру матрицы W.

Ниже мы рассмотрим наиболее важные и достаточно часто встречающиеся на практике виды структур матрицы W, соответствующие моделям с гетероскедастичностью и автокоррелирумостью остатков.