Ошибки спецификации
Построение работоспособной эконометрической модели возможно при условии достаточно хорошей (правильной) спецификации уравнения регрессии. Выполнение условия правильной спецификации модели базируется на надежности выводов предмодельного качественного анализа исследуемого объекта, а также на результатах методик, направленных на устранение или корректировку ошибок спецификации, которые весьма нередки, особенно на начальном этапе эконометрического анализа.
К основным ошибкам спецификации следует отнести выбор неправильной функциональной формы модели, отбрасывание (невключение) значимой переменной, добавление (включение) незначимой переменной.
Выбор неправильной функциональной формы модели, например, использование вместо правильной линейной модели полиномиального уравнения с теми же переменными, приводит к серьезным отрицательным последствиям. Обычно такая ошибка вызывает ухудшение статистических свойств оценок коэффициентов регрессии и прогнозных качеств модели. С точки зрения регрессионного анализа в данном случае наблюдается нарушение условий Гаусса-Маркова для случайных отклонений.
Критерием прогнозных качеств оцененной регрессионной модели может служить следующее соотношение:
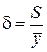 , (4.24)
, (4.24)
где 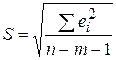 – стандартная ошибка регрессии,
– стандартная ошибка регрессии, 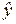 - среднее значение зависимой переменой уравнения регрессии. Величина d определяет относительную ошибку прогноза.
- среднее значение зависимой переменой уравнения регрессии. Величина d определяет относительную ошибку прогноза.
Если возможно провести сравнение моделей различной функциональной формы, но содержащих одинаковый набор переменных, то выбирается модель с наибольшим скорректированным коэффициентом детерминации 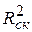 и наименьшей величиной d.
и наименьшей величиной d.
Для случая парной (однофакторной) регрессионной модели подбор функциональной формы обычно осуществляется по виду расположения точек наблюдений на корреляционном поле. Для оцененной парной регрессии о правильности выбора функциональной формы можно судить по значениям коэффициента детерминации и средней ошибки аппроксимации. Для множественной регрессии ситуация более неоднозначна, так как графическое представление статистических данных в этом случае невозможно. Здесь детальный анализ адекватности функциональной формы модели и ошибок спецификации в целом может быть проведен на основе специальных тестов, подробное описание которых выходит за рамки данной книги. Суть тестов по обнаружению неправильной спецификации модели основана на исследовании поведения случайных отклонений еi [6].
В целом следует заметить, что даже правильно специфицированная на данном этапе эконометрическая модель должна постоянно совершенствоваться, исходя из меняющихся условий функционирования экономических систем. Совершенствование модели с целью лучшего соответствия экспериментальным данным может приводить к изменению вида функциональных связей между переменными и набора факторов-аргументов.
Рассмотрим следующую, достаточно распространенную ошибку спецификации, которая характеризуется как невключение значимой переменной в уравнение регрессии. Пусть, например, объясняемая переменная Y линейно зависит от двух факторов-аргументов Х1 и Х2, и истинная модель имеет вид:
Y = b0 + b1Х1 + b2Х2 + e. (4.25)
Однако исследователь, в силу недостатка информации об экономическом объекте или неправильной ее обработки, ошибочно считает, что на переменную Y реально воздействует лишь переменная Х1 и оценивает регрессию
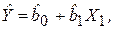 (4.26)
(4.26)
для которой 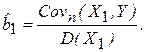
Последствия допущенной ошибки выражаются в том, что оценки параметров, полученные с помощью МНК по уравнению (4.26), являются смещенными ( 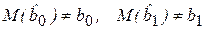 ) и несостоятельными даже при неограниченно большом числе наблюдений. Покажем это для оценки
) и несостоятельными даже при неограниченно большом числе наблюдений. Покажем это для оценки 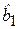 .
.
С учетом выполнения (4.25) коэффициент 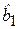 вычисляется по формуле:
вычисляется по формуле:
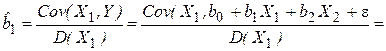

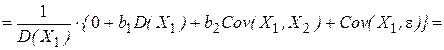
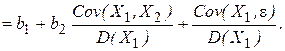 (4.27)
(4.27)
По условию классической регрессионной модели переменные Х1 и Х2 являются детерминированными (нестохастическими). Тогда Cov(Х1, e) = 0 и для математического ожидания оценки параметра 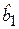 получим следующее выражение:
получим следующее выражение:
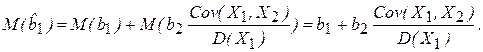 (4.28)
(4.28)
Таким образом, в соответствии с (4.28) оценка 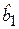 обладает смещением относительно истинного параметра, которое определяется величиной
обладает смещением относительно истинного параметра, которое определяется величиной 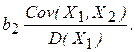 Знак (направление) смещения зависит от знаков величин
Знак (направление) смещения зависит от знаков величин 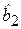 и Cov(Х1, Х2). Например, при положительном параметре
и Cov(Х1, Х2). Например, при положительном параметре 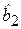 и положительной корреляции между Х1 и Х2 оценка
и положительной корреляции между Х1 и Х2 оценка 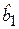 будет завышать истинное значение параметра
будет завышать истинное значение параметра 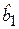 .
.
Отметим, что невключение переменной существенно отражается на коэффициенте детерминации R2, завышая влияние фактора-аргумента Х1 на объясняемую дисперсию результирующей переменной Y. Смещенные оценки параметров модели могут приводить к ложным выводам соответствующих статистических тестов (статистических поверок гипотез).
Рассмотрим следующую ситуацию. Пусть уравнение
Y = b0 + b1Х1 + e (4.29)
представляет истинную модель, а мы заменяем ее более сложной моделью (4.25), совершая при этом ошибку добавления (включения) незначимой переменной.
Последствия данной ошибки не являются столь серьезными, как в предыдущем случае. Оценки параметров 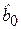 и
и 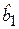 , найденные для модели (4.25), остаются несмещенными и состоятельными. Этот факт может подтолкнуть исследователя к включению в модель большого числа недостаточно значимых объясняющих переменных с целью получить лучшую подгонку под имеющиеся экспериментальные данные. Однако включение незначимых переменных приводит к увеличению стандартных ошибок коэффициентов, т. е. их оценки становятся неэффективными. Кроме того, неоправданное увеличение числа регрессоров в модели приводит к ее неустойчивости вследствие проявления мультиколлинеарности.
, найденные для модели (4.25), остаются несмещенными и состоятельными. Этот факт может подтолкнуть исследователя к включению в модель большого числа недостаточно значимых объясняющих переменных с целью получить лучшую подгонку под имеющиеся экспериментальные данные. Однако включение незначимых переменных приводит к увеличению стандартных ошибок коэффициентов, т. е. их оценки становятся неэффективными. Кроме того, неоправданное увеличение числа регрессоров в модели приводит к ее неустойчивости вследствие проявления мультиколлинеарности.
Вывод об увеличении стандартных ошибок и неэффективности оценок можно проиллюстрировать формулами (2.22) и (3.26) расчета дисперсий оценок коэффициентов для уравнений (4.29) и (4.25) соответственно:
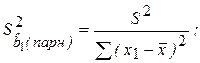
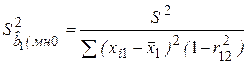 .
.
Здесь S2 - дисперсия случайных отклонений; r12 – коэффициент корреляции между объясняющими переменными Х1 и Х2.
Таким образом, дисперсия для парной регрессии 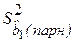 оказывается меньше дисперсии для множественной регрессии
оказывается меньше дисперсии для множественной регрессии 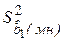 , которая неограниченно возрастает при стремлении r12 к 1.
, которая неограниченно возрастает при стремлении r12 к 1.
Вопросы и упражнения для самопроверки
1. Что понимается под спецификацией модели?
2. Каковы признаки качественной регрессионной модели?
3. Приведите примеры нелинейных моделей в экономике.
4. Опишите методы линеаризации моделей.
5. Какие требования предъявляются к свойствам случайных отклонений при линеаризации?
6. Что отражает производственная функция Кобба-Дугласа; как можно построить и оценить модели на ее основе?
7. По имеющимся статистическим данным оцените параметры b0 и b1 следующей экспоненциальной модели: 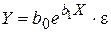 .
.
| Х | |||
| Y | 0,85 | 0,45 | 0,4 |
8. Как формализованно можно представить качественные факторы в регрессионной модели?
9. Что описывают и как выражаются фиктивные переменные?
10. Сформулируйте правило использования фиктивных переменных в случае нескольких (k) градаций качественного признака.
11. Опишите, как можно использовать фиктивные переменные в сезонном анализе.
12. С помощью фиктивной переменной напишите уравнение парной регрессии, соответствующее структурному изменению, произошедшему в момент времени 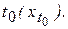
13. Напишите уравнение множественной регрессионной модели, отражающей зависимость средней цены на двухкомнатную квартиру (Y) от следующих факторов: жилая площадь; площадь нежилых помещений, включая кухню; расстояние от центра города; расположение квартиры (первый или последний этаж); строительный материал (дом кирпичный или панельный); наличие или отсутствие лифта.
14. Сформулируйте цель и последовательность проведения теста Г. Чоу.
15. Как можно проверить гипотезу о том, что величина дохода влияет на «склонность к потреблению»?
16. Перечислите основные виды ошибок спецификации.
17. Охарактеризуйте основные виды ошибок спецификации и их последствия.
18. Как можно обнаружить ошибки спецификации?
Дата добавления: 2016-06-02; просмотров: 1893;
