Фиктивные переменные в регрессионных моделях

В линейных и сводящихся к линейным регрессионных моделях, оцениваемых по МНК, мы рассматривали влияние факторов-аргументов, задаваемых количественно (производительность труда, цена, доход и т. п.). Однако на практике достаточно часто возникает необходимость учитывать влияние качественных факторов на исследуемый экономический показатель.

Наиболее распространенные качественные факторы (признаки) – профессия, пол, образование, фактор сезонности, тип потребительского поведения, отдельные регионы.

Отметим, что многие качественные факторы имеют два или несколько достаточно четко выраженных уровней (градаций). Например, пол – мужской, женский; образование – среднее, высшее; и т. д. Чтобы рассмотреть влияние качественного фактора, нужно построить и оценить регрессионные модели для каждого уровня качественного признака, а затем изучать различие между ними. Однако возможен и другой, более информативный подход, позволяющий оценивать влияние значений количественных факторов-аргументов и уровней качественных признаков с помощью одного уравнения регрессионной модели. Этот подход связан с введением в модель специальной переменной, которая отражает два противоположных состояния качественного фактора и носит название фиктивной (искусственной, манекенной) переменной.

Фиктивная переменная (D) может выражаться в двоичной форме, например:

.

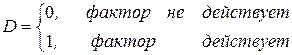Например, D = 0, если сотрудник фирмы не имеет высшего образования; D = 1, если сотрудник имеет высшее образование; D = 0, если в обществе имеются инфляционные ожидания; D = 1 если инфляционных ожиданий нет.

Введение фиктивных переменных позволяет рассматривать в регрессионном анализе, кроме моделей, содержащих количественные объясняющие переменные Х_j, модели, включающие лишь качественные факторы D_j, либо те и другие одновременно. Модели, в которых используются фиктивные переменные, рассматриваются как регрессионные модели с переменной структурой, поскольку качественные признаки могут существенно влиять на структуру линейных связей между переменными, например, приводить к скачкообразному изменению коэффициентов регрессии.

Если рассматриваемый качественный признак имеет несколько (k) уровней, то для анализа используется (k - 1) фиктивных переменных. Так, например, для выявления влияния фактора сезонности (четыре сезона) на определенный экономический показатель можно ввести только три фиктивные переменные D₁, D₂, D₃:

d_1t = 1, если месяц t является зимним, d_1t = 0 в остальных случаях;

d_2t = 1, если месяц t является весенним, d_2t = 0 в остальных случаях;

d_3t = 1, если месяц t является летним, d_3t = 0 в остальных случаях.

Данная ситуация может быть отражена регрессионной моделью

y_t = b₀ + g₁d_1t + g₂d_2t + g₃d_3t + e_t, (4.14)

где t - индекс времени (месяца); g - коэффициенты при фиктивных переменных.

Следует заметить, что мы не должны вводить четвертую фиктивную переменную D₄, относящуюся к осеннему периоду, иначе для любого месяца t будет выполняться тождество d_1t + d_2t + d_3t + d_4t = 1, что означает линейную зависимость регрессоров (мультиколлинеарность) в уравнении (4.14), и, как следствие, невозможность применения МНК для определения параметров модели.

В некоторых случаях фиктивные переменные могут быть использованы для объяснения поведения зависимой (результирующей) переменной Y. Например, если исследовать зависимость наличия автомобиля от дохода или пола субъекта, то зависимая переменная имеет как бы два возможных значения: 0, если машины нет, и 1, если машина есть. Однако непосредственное использование обычного МНК для оценки моделей данного типа не представляется возможным в силу невыполнимости основных предпосылок Остроградского-Гаусса. Поэтому для определения коэффициентов в этом случае используются другие методы, в частности взвешенный метод наименьших квадратов (ВМНК)*.

В качестве наиболее простого примера обычных моделей с объясняющей фиктивной переменной рассмотрим модель, связанную с уровнем образования. Пусть y_i – размер заработной платы t-го работника. Введем в рассмотрение фиктивную переменную:

.

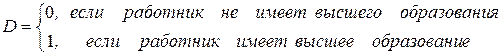Тогда зависимость можно выразить моделью парной регрессии

y_i = b₀ + gd_i + e_i

или в общем виде

Y = b₀ + gD + e_. (4.15)

Принимая модель (4.15), мы считаем, что b₀ определяет среднюю заработную плату при отсутствии высшего образования и b₀ + g – при его наличии. Таким образом, величина g интерпретируется как среднее изменение зарплаты при переходе из одной категории (без высшего образования) в другую (с высшим образованием). Проверяя статистическую значимость коэффициента g с помощью t-статистики, мы проверяем предположение о несущественном различии в заработной плате между категориями.

Наиболее применимы на практике модели, содержащие как количественные, так и качественные объясняющие переменные. Например, пусть Y - заработная плата сотрудника фирмы, Х -стаж работы сотрудника, D - пол сотрудника. В данном случае рассматривается модель:

Y = b₀ + b₁Х + gD + e. (4.16)

Фиктивная переменная D будет принимать следующие значения:

.

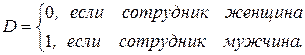Тогда ожидаемое значение заработной платы сотрудников при Х годах стажа работы будет определяться двумя уравнениями:

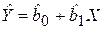- для женщины (4.17)

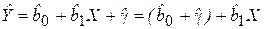- для мужчины. (4.18)

В данном случае заработная плата является линейной функцией от стажа работы (рис. 4.3а), которая изменяется и для мужчин, и для женщин с одним и тем же коэффициентом пропорциональности 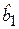. Различие в моделях (4.17) и (4.18) заключается в свободных членах, которые отличаются на величину 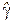. Имея статистическую информацию, можно определить оценки параметров модели методом наименьших квадратов. 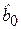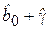Проверка статистической значимости коэффициентов и ( ) позволяет установить, имеется ли в действительности в данной фирме дискриминация по половому признаку. Если коэффициенты окажутся статистически значимыми, то дискриминация есть. При g > 0 она будет в пользу мужчин, при g < 0 – в пользу женщин.

Рассмотренные выше регрессионные модели (4.17) и (4.18) отражали влияние качественного признака (фиктивных переменных) только на величину свободного члена уравнения регрессии. В более сложных моделях может быть учтено влияние качественных факторов на сами параметры при объясняющих переменных. В случае парной регрессии это приводит к изменению наклона линии модели (рис. 4.3б).

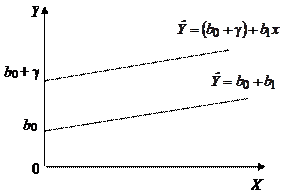
а б

Рис. 4.3.

Рассмотрим удельное потребление (Y) некоторого товара или услуги в зависимости от дохода потребителя (Х) При моделировании введем качественную градацию типа потребительского поведения, которая будет отражена одной фиктивной переменной D₁:

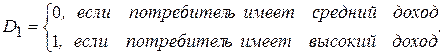
Естественно предположить, что фактор потребительского поведения, отражаемый фиктивной переменной D₁, влияет не только на количество потребляемого товара (продукта), но и на «склонность к потреблению», т. е. на величину коэффициента b₁ В этом случае общую модель можно записать в следующем виде:

Y = b₀ + b₁Х + g₁D₁ + g₂D₁Х + e. (4.19)

Из модели (4.19) в результате действия фиктивной переменной образуются два уравнения регрессии

Y = b₀ + b₁Х +e - если средний доход, (4.20)

Y = (b₀ + g₁) + (b₁ + g₂)Х + e - если высокий доход. (4.21)

Анализируемая модель схематически отражена на рис. 4.3б. Здесь х₀ определяет некоторый уровень дохода, превышение которого приводит к изменению структуры модели в соответствии с переходом от одного типа потребительского поведения к другому.

Модель (4.19) может быть усложнена за счет действия других реальных факторов, например, фактора сезонности. В простейшем случае фиктивная переменная D₂ может быть выражена следующим образом:

,

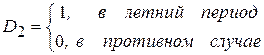что соответствует, например, удельному потреблению прохладительных напитков или пива. С учетом фактора сезонности модель примет вид:

Y = b₀ + b₁Х + g₁D₁ + g₂D₁Х + g₃D₂ + e. (4.22)

В данной модели фактор сезонности D₂ влияет на количество потребляемого продукта, но не влияет на «склонность к потреблению», т. е. на коэффициент b₁.

В целом следует заметить, что фиктивные переменные являются простым и, в то же время, весьма гибким инструментом эконометрических исследований, позволяющим изучать влияние различных качественных факторов на экономические показатели. Способ включения фиктивных переменных в модель основывается на априорной информации относительно влияния соответствующих качественных факторов на зависимую переменную.

Тест Г. Чоу

В том случае, когда фиктивная переменная действует на коэффициент при объясняющей переменной, линия модели отличается от той, которая была до уровня х₀ (рис. 4.3б), что соответствует разбиению выборочных данных на две части (группы) и рассмотрению отдельных уравнений регрессии по каждой выборке (подвыборке).

В практике эконометриста достаточно часто возникает вопрос, имеет ли смысл разбивать выборку на части и строить так называемою кусочно-линейную модель с фиктивными переменными (рис. 4.3б) или ограничиться «обыкновенной» общей регрессией для всего диапазона точек наблюдений?

Для ответа на этот вопрос обычно используется тест (критерий) Грегори Чоу, суть которого заключается в следующем. Пусть общая выборка имеет объем n Через S₀ обозначим сумму квадратов отклонений 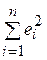выборочных данных от их модельных оценок, полученных по общему уравнению регрессии. Разобьем выборку на две подвыборки объемами n₁ и n₂ соответственно (n₁ + n₂ = n). Будем считать, что для каждой подвыборки можно построить уравнения регрессии одного вида, но с разными коэффициентами b. Через 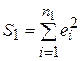и 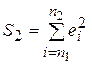обозначим соответствующие суммы квадратов отклонений. Далее рассмотрим некоторые соотношения.

Очевидно, что равенство S₀ = S₁ + S₂ выполняется лишь при совпадении коэффициентов регрессии для всех трех уравнений. Тогда отклонение S₀ - (S₁ + S₂) может быть использовано как показатель улучшения качества модели при разбиении интервала наблюдений на две подвыброки, так как чем сильнее различие в поведении Y для каждой из подвыборок, тем больше значение S₀ будет превосходить сумму S₁ + S₂. Следовательно, отношение [S₀ - (S₁ + S₂)]/(m + 1) будет определять оценку уменьшения дисперсии регрессии за счет построения двух уравнений вместо одного.

При разбиении общей выборки число степеней свободы сократится на (m + 1), т. к. теперь вместо (m + 1) параметра объединенной регрессионной модели необходимо оценивать (2m + 2) коэффициента двух регрессий. В данном случае соотношение (S₁ + S₂)/(n - 2m - 2) выражает необъясненную дисперсию зависимой переменной при рассмотрении двух регрессий.

Приведенные выше рассуждения позволяют сделать вывод о том, что общую выборку целесообразно разбивать на два интервала только в том случае, если соответствующее уменьшение дисперсии будет значимо больше оставшейся необъясненной дисперсии. Этот вывод может быть основан на стандартной процедуре сравнения дисперсий на основе F-статис­тики, наблюдаемое значение которой для данного анализа имеет вид:

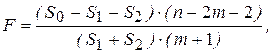(4.23)

где m - число количественных объясняющих переменных в уравнениях регрессии (m - одинаково для всех трех уравнений модели).

Если F_набл < F_кр при заданном уровне значимости a и соответствующих числах степеней свободы v₁ = m + 1 и v₂ = n - 2m - 2, то можно считать, что различие между S₀ и S₁ + S₂ статистически незначимо и нет смысла разбивать уравнение модели на части путем введения фиктивных переменных. Следует заметить, что фактически мы тестируем гипотезу Н₀ о равенстве коэффициентов b уравнений регрессии, построенных по каждой подвыборке. Если нулевая гипотеза Н₀ верна, то две регрессионные модели можно объединить в одну, построенную по выборке объема n = n₁ + n₂.