Дискретные зависимые переменные
Ранее мы рассматривали переменные в моделях, которые являются независимыми и могут принимать дискретные значения. Например Хо или Х1 (фиктивные переменные), а вот зависимая переменная У предполагалась количественной. В то же время довольно часто интересует нас величина У, являющаяся дискретной. Выделим несколько типичных ситуаций.
1.Выбор из нескольких альтернатив. Например: голосование на выборах (зависимая переменная – выбор из нескольких кандидатов); решение работать или не работать; выбор профессии, форма собственности предприятия и т.д.
Если есть только 2 возможности – бинарный выбор, то результат наблюдения, обычно описывающийся переменной, принимающей 2 значения 0 или 1. (Ехать не ехать, голосовать или нет)
0 – нет
1 – да
В общем виде результат может быть записан как [1…k]
2.Ранжированный выбор – результат состоит из нескольких альтернатив. [1…m]
(Уровень образования – незаконченное среднее, среднее, среднетехническое, высшее; доход семьи – низкий, высокий, очень высокий).
Соответствующая переменная ряда называется порядковой или ранжированной.
3.Количественная целочисленная характеристика. (Число предприятий, число выданных патентов, количество возвратов товара и т.д.)
Для таких моделей с дискретной зависимой переменной при построении модели формально возможно применение МНК для нахождения оценок коэффициентов.
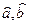
Остатки модели не будут близки к нормальному распределению, не будут случайными, поэтому сами оценки параметров a и b будут плохие, по ним получается никакой прогноз.
Решение проблемы
Строится модель бинарного и множественного выбора. Рассматриваются модели бинарного и множественного выбора на примере покупки автомобиля.
У=1 – купила
У=0 – не купила
- в определенные периоды времени.
Например в периоды рекламы ясно, что решение о покупке автомобиля влияют самые разные факторы: доход, количество человек в семье, возраст членов семьи, место проживания, уровень образования членов семьи и т.д. Эти факторы можно представить с помощью вектора Х=(Х1…Хк). Выдвигая различные предположения о характере зависимости У от Х, мы будем получать разные модели. Далее мы рассмотрим 3 модели: 1)Линейная модель вероятности
2)logit-model
3)probit-model
Начнем с линейной модели вероятности. Воспользуемся обычной регрессионной моделью, где b - вектор неизвестных коэффициентов, Х – вектор столбец. У принимает значение 0 или 1, а Е(e)=0 (для построения МНК)
Тогда можно записать, что Е(У)=1*Р(У=1)+0*Р(У=0)=Е(х’b)+0’=x’E(b)=x’b
Мы получили, что вероятность того, что У=1 равно x’b. Это и есть линейная модель верояности.
Основным недостатком этой модели является тот факт, что прогнозные значения вероятности Р(У)=1 могут лежать вне отрезка [0,1], что, конечно же не подлежит разумной интерпритации.
Справиться с недостатком этой модели можно, если предположить, что вероятность равна некоторой функции Р(У=1)=F(x’b), где F(*) – некоторая функция, принадлежащая [0;1].
Наиболее часто в качестве функции F используют либо функцию нормального распределения (probit) либо функцию логического распределения (logit). Результатом применения и построения logit-probit модели, является прогноз вероятности того, что У примет значение 1.
Например: с помощью logit-probit модели можно построить модель вероятности банкротства предприятия. Зависимая переменная – вероятность банкротства, независимые факторы – факторы финансового состояния предприятия.
1 – предприятие в течение 3-х месяцев стало банкротом
0 – не стало.
В данной модели оценки коэффициентов находятся с помощью, например, метода максимума правдоподобия, а основная проблема – определить пороговое значение вероятности, после которой надо волноваться.
Дата добавления: 2016-08-07; просмотров: 1737;
