Обнаружение автокорреляции
Большинство тестов на наличие автокорреляции основаны на достаточно простой идее: если корреляция во времени присутствует между случайными отклонениями et, то она должна проявляться и в их оценках et, получаемых при использовании обычного МНК. Наиболее распространенным примером реализации данного подхода является тест (критерий) Дарбина-Уотсона, который определяет наличие автокорреляции между соседними отклонениями. Этот критерий основан на применении статистики Дарбина-Уотсона (DW), определяемой соотношением:
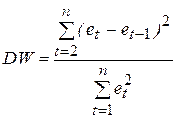 . (5.10)
. (5.10)
Покажем, что статистика Дарбина-Уотсона связана с выборочным коэффициентом корреляции между соседними отклонениями r следующим образом:
DW » 2(1 - r). (5.11)
Преобразуем соотношение (5.10)
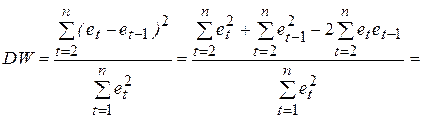
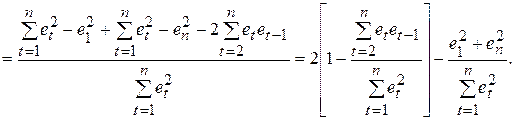 (5.12)
(5.12)
При достаточно больших выборках сумма 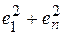 значительно меньше
значительно меньше 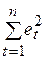 , поэтому последним членом в формуле (5.12) можно пренебречь. Тогда получим:
, поэтому последним членом в формуле (5.12) можно пренебречь. Тогда получим:
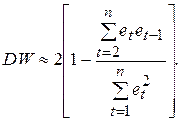 (5.13)
(5.13)
Учитывая, что математическое ожидание M(et) = 0, запишем формулу для вычисления выборочного коэффициента корреляции:
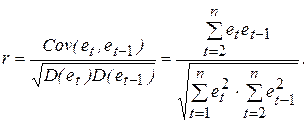
При большом числе наблюдений n суммы 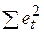 и
и 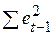 будут практически одинаковы. Поэтому выборочный коэффициент корреляции r можно приближенно представить в виде:
будут практически одинаковы. Поэтому выборочный коэффициент корреляции r можно приближенно представить в виде:
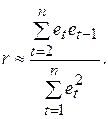 (5.14)
(5.14)
Из сравнения выражений (5.13) и (5.14) следует приближенное равенство (5.11).
Согласно формуле (5.11) значения статистики Дарбина-Уотсона могут находиться в пределах 0 £ DW £ 4 и указывают на наличие либо отсутствие автокорреляции. Действительно, если автокорреляция отсутствует, то выборочный коэффициент корреляции между соседними отклонениями r » 0 и значение статистики DW будет близко к двум, что соответствует независимости случайных отклонений. Близость наблюдаемого значения статистики к нулю указывает на наличие положительной автокорреляции, к четырем – отрицательной автокорреляции. Следует заметить, что непосредственное использование статистики DW в схеме проверки статистических гипотез (H0 : r = 0, H1 : r > 0, r < 0) не представляется возможным. Проблема состоит в том, что распределение статистики DW зависит не только от числа наблюдений n и количества регрессоров m, но и от значений объясняющих переменных. В этом случае пороговые (критические) значения статистики указать невозможно. Однако Дарбин и Уотсон доказали, что для статистики существуют две границы (du - верхняя, dl - нижняя), которые зависят только от n, m и выбираемого уровня значимости a. Значения этих границ статистики DW затабулированы (см. Приложение 6) и могут быть использованы для проверки нулевой гипотезы H0 об отсутствии автокорреляции.
Приведем общую схему применения теста (критерия) Дарбина-Уотсона.
1. По построенному с помощью МНК эмпирическому уравнению регрессии:
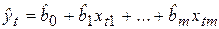
определяются значения отклонений (остатков) 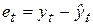 для каждого конкретного наблюдения t, t = 1, 2, …, n.
для каждого конкретного наблюдения t, t = 1, 2, …, n.
2. По формуле (5.10) на основе полученных данных рассчитывается наблюдаемое значение статистики DW.
3. По таблице критических значений статистики DW определяются два числа dl и du и делаются выводы о наличии автокорреляции по правилу, отраженному следующей таблицей.
Таблица 5.1
| Значение статистики DW | Вывод |
| 0 < DW < dl | Гипотеза H0 отвергается, есть положительная автокорреляция |
| dl < DW < du | Неопределенность |
| du < DW < 4 - du | Гипотеза H0 не отвергается (автокорреляция отсутствует) |
| 4 - du < DW < 4 - dl | Неопределенность |
| 4 - dl < DW < 4 | Гипотеза H0 отвергается, есть отрицательная автокорреляция |
Статистика Дарбина-Уотсона приводится во всех компьютерных эконометрических пакетах как важная характеристика качества регрессионной модели. Несмотря на то, что тест Дарбина-Уотсона наиболее распространен в регрессионном анализе, он обладает рядом ограничений и недостатков. Его основными недостатками являются наличие зоны неопределенности для значений статистики, когда нет оснований ни принимать, ни отвергать гипотезу H0 об отсутствии автокорреляции, а также неприменимость для так называемых авторегрессионных моделей*, содержащих в составе объясняющих переменных зависимую переменную с временным лагом в один период.
Дата добавления: 2016-06-02; просмотров: 1136;
