Парная линейная регрессия.
Связь между показателем Y и фактором Х с учетам возможных отклонений запишем в виде 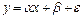 , где
, где 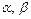 – неизвестные параметры регрессии,
– неизвестные параметры регрессии, 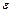 – случайная величина, которая характеризует отклонение параллельно оси
– случайная величина, которая характеризует отклонение параллельно оси 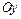 наблюдаемых точек от линии регрессии.
наблюдаемых точек от линии регрессии.
Таким образом, показатель Y представляется в виде систематической составляющей 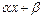 и случайной составляющей величины
и случайной составляющей величины 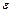 . Зависимость
. Зависимость 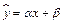 , которая характеризует среднее значение показателя Y для данного значения фактора Х, называется регрессией. Можно сказать иначе. Регрессия характеризует тенденцию изменения показателя, обусловленную изменением фактора. Зависимость
, которая характеризует среднее значение показателя Y для данного значения фактора Х, называется регрессией. Можно сказать иначе. Регрессия характеризует тенденцию изменения показателя, обусловленную изменением фактора. Зависимость 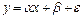 характеризует индивидуальное значение показателя Y с учетом возможных отклонение от средних значений.
характеризует индивидуальное значение показателя Y с учетом возможных отклонение от средних значений.
Действительные значения параметров вычислить нельзя, так как мы имеем ограниченное число наблюдений, поэтому полученные расчетные значения параметров 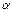 и
и 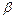 являются статистическими оценками действительных параметров
являются статистическими оценками действительных параметров 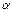 и
и 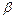 . Обозначим оценки параметров соответственно через а и b. Тогда уравнение парной регрессии
. Обозначим оценки параметров соответственно через а и b. Тогда уравнение парной регрессии 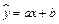 (рис.1) будет оценкой модели
(рис.1) будет оценкой модели 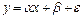 .
.
 y
y

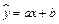
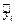
0 xi x
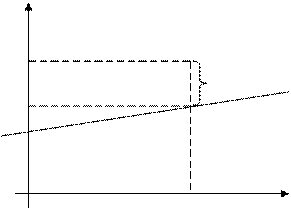
Рис. 1.1. Отклонение теоретических значений от фактических.
Рассмотрим разность  и
и 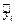 , (i=1, n):
, (i=1, n):
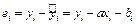 ,
,
где  – фактические,
– фактические, 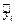 – расчетные значения показателя,
– расчетные значения показателя, 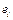 – отклонение наблюдаемой точки (
– отклонение наблюдаемой точки ( 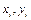 ) от точки (
) от точки ( 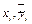 ) сглаживающей кривой. Метод наименьших квадратов заключается в таком подборе оценок параметров регрессии а и b, для которых сумма квадратов отклонений наблюдаемых значений показателя от сглаживаемых будет минимальной, т.е. необходимо минимизировать
) сглаживающей кривой. Метод наименьших квадратов заключается в таком подборе оценок параметров регрессии а и b, для которых сумма квадратов отклонений наблюдаемых значений показателя от сглаживаемых будет минимальной, т.е. необходимо минимизировать 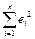 :
:
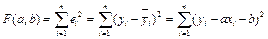
Необходимым условием экстремума функции двух переменных 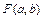 является равенство нулю частных производных этой функции по переменным а и b:
является равенство нулю частных производных этой функции по переменным а и b:

Отсюда имеем:
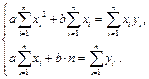 (1.1)
(1.1)
Система является линейной относительно переменных а и b. Решая ее, получим:
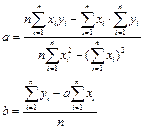 (1.2)
(1.2)
Функция 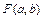 имеет единственную критическую точку.
имеет единственную критическую точку.
Вычислим вторые производные в найденной критической точке и обозначим их А, В, С:
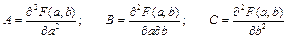 .
.
Если 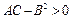 и
и 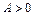 , то в точке (
, то в точке ( 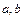 ) функция
) функция 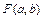 имеет минимум. Проверим это достаточное условие:
имеет минимум. Проверим это достаточное условие:
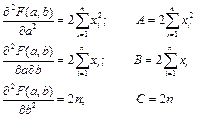
Вычислим 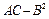 :
:
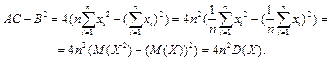
Здесь 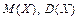 соответственно математическое ожидание и дисперсия случайной величины Х. Если случайная величина Х не является постоянной, то
соответственно математическое ожидание и дисперсия случайной величины Х. Если случайная величина Х не является постоянной, то 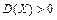 , поэтому
, поэтому 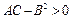 . Поскольку
. Поскольку 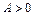 , то решение (1.2) системы (1.1) является точкой минимума функции
, то решение (1.2) системы (1.1) является точкой минимума функции 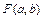 .
.
Дата добавления: 2016-05-11; просмотров: 649;
