Коэффициент корреляции.

После того, как определены неизвестные параметры линейной регрессии, попытаемся оценить тесноту связи между зависимой переменной у и независимой х, т.е. попытаемся ответить на вопрос, насколько значимым является влияние переменной х на у. Простейшим критерием, который дает количественную оценку связи между двумя показателями, является выборочный коэффициент корреляции, который вычисляется по формуле

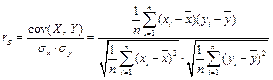(1.7)

где 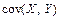– коэффициент ковариации между х и у; 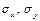– средние квадратические отклонения случайных величин X и Y.

Сумма квадратов отклонений 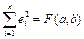называется остаточной дисперсией. Установим связь между этой величиной и коэффициентом корреляции. В силу формулы (1.5)

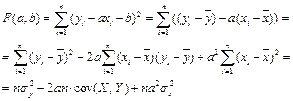
В силу (1.4 ) и (1.7) 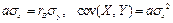, поэтому

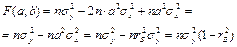
Если 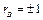, то 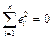и поэтому случайные величины Х и Y связаны линейной функциональной зависимостью.

Если 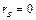, то 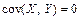и случайные величины являются независимыми. Таким образом, коэффициент корреляции служит мерой тесноты линейной корреляционной зависимости между случайными величинами Х и Y. Если абсолютная величина коэффициента 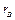близка к единице, то случайные величины связаны тесной линейной корреляционной зависимостью; если абсолютная величина 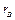близка к нулю, то линейная корреляционная зависимость отсутствует. Однако такая оценка является только качественной.