Понятие доверительного интервала. Доверительные интервалы для единичного замера и математического ожидания.

В математической статистике используются два метода оценки экспериментальных данных: точечный и интервальный.

В точечном методе ищутся характеристики 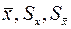в соответствии с рассмотренным выше методом.

Недостатки точечного метода состоят в следующем. Так как сама выборка является случайной, то случайными будут и полученные на ее основе оценки. Если данный, и тем более другой, исследователь проведет новую серию опытов на том же объекте, с теми же приборами, то получит новые результаты, которые в общем случае будут характеризоваться другими значениями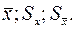

При использовании точечного метода остаются неизвестными вероятность и точность результат обработки.

Интервальный метод оценки свободен от таких недостатков. В последнее время он нашел широкое распространение. Сущность его составляет понятие доверительного интервала /5/.

Предположим, что мы имеем какую – либо генеральную совокупность. Если распределение величин в ней подчиняется нормальному закону, то график плотности вероятностей будет иметь вид, приведенный на рис. 2.3 .

Известно, что

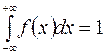
Выделим вокруг 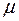какой – либо интервал, например 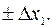Тогда

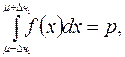
где p - вероятность того, что данный единичный замер попадет в интервал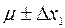

Эта вероятность называется доверительной для интервала 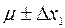, а сам интервал – доверительным с соответствующей вероятностью. Величина 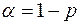называется уровнем значимости или риском.

Например, для интервала 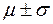доверительная вероятность P = 0.68269, а риск попадания единичного замера за его пределы 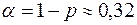.Это очень большой риск. Интервальные оценки осуществляют с большей вероятностью. Вероятность попадания замера в интервал 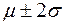составляет 0.955.

Риск 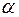=0.045 уже приемлем. Такой интервал широко используется в инженерной практике. Для интервала 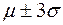риск составляет 0.0027 , т. е. весьма мал. Интервалы 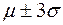используются только в весьма ответственных расчетах.

Понятие «доверительный интервал» тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. Из определения следует, что если манометр с максимальным значением по шкале 100кгс/см² имеет точность 1% , то его абсолютная предельная погрешность 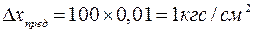В настоящее время в измерительной технике в большинстве отраслей промышленности под предельной погрешностью прибора понимается величина, равная двум среднеквадратическим отклонениям, т. е. 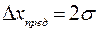, что соответствует доверительной вероятности Р=0,955 и риску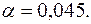

Таким образом, для манометра, о котором шла речь выше,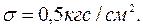

До сих пор говорилось об интервальных оценках при нормальном распределении бесконечного числа замеров. На практике, как уже отмечалось, мы имеем дело с выборкой, включающей обычно два – пять замеров. При этом для оценок необходимо использовать распределения Стьюдента.

Широко используют интервальные оценки для единичного замера и математического ожидания.

Доверительный интервал для единичного замера определяется

выражением

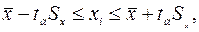(2.9)

а для математического ожидания

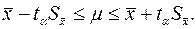
(2.10)

В выражении (2.9) и (2.10) 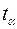- критерий Стьюдента при доверительной вероятности 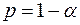или уровне значимости .

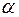Величина берется из таблицы для соответствующей доверительной вероятности в зависимости от числа степеней свободы .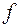

Таблица 2.3

Значения критерия Стьюдента для уровня значимости 0,05

f
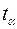….	12.706	4.303	3.182	2.776	2.571	2.447	2.306	2.228	2.086	2.042	2.00

Пример.По шести замерам подачи насоса 105; 95; 100; 99; 103, 98м³/час определить интервальную оценку для математического ожидания. Ранее было установлено, что для данной выборк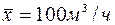и и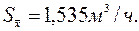

Для числа степеней свободы 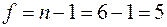из табл.2.3 критерий Стьюдента 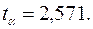Таким образом,

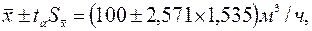
или подача насоса с вероятностью 95%

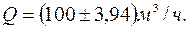
В таком виде и следует приводить конечный результат.