Результаты замеров диаметра стержня

Диаметр стержня, мм	49,0 49,4	49,4 49.8	49,8 50,2	50,2 50,6	50.6 51.0	51.0 51,4	51,4 51,8
Количество приходящихся замеров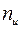

Гистограмма распределения замеров приведена на рисунке 2.1. Если истинное значение диаметра стержня составляет 50,4мм , то нетрудно от замеров перейти к ошибкам. Разделив число замеров в каждом интервале на всю выборку (в условиях примера на 56), получим вероятность попадания измерений в соответствующий интервал. Соединив средние точки интервалов прямыми, получим полигон распределений, являющийся оценкой плотности вероятностей. Пунктирной прямой на рис.2.1 показано изменение плотности вероятностей для нормального распределения ошибок. Рисунок свидетельствует о хорошем соответствии распределения ошибок в выборке нормальному закону.

Рис. 2.1. Гистограмма распределения замеров

Рис. 2.2. Равномерный закон распределения замеров

Рис. 2.3. Доверительный интервал

Разработаны методы, позволяющие проверить соответствие данных выборки нормальному распределению без построения гистограммы.

Для нормального распределения характерна симметричность – положительные и отрицательные ошибки встречаются одинаково часто. В инженерных экспериментах в большинстве случаев можно считать, что распределение ошибок подчиняется нормальному закону.

Нормальное распределение характеризуется двумя параметрами: генеральным средним (математическим ожиданием) … 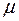…. и генеральным средним квадратическим отклонением … 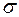… . Квадрат… 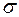…. называется генеральной дисперсией.

Величина… 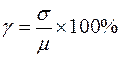…. называется коэффициентом вариации.

Математическое ожидание выступает как наиболее вероятное значение измеряемой величины. Дисперсия же является численной характеристикой степени рассеяния. Обычно проводится два – пять опытов. По ним определяются оценки для … 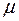. . и … 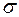… . Оценкой для математического ожидания является выборочное среднее

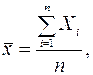(2.3)

где 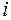- порядковый номер опыта;

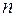- число повторных опытов.

Например, оценкой для математического ожидания подачи насоса при x₁=105м³/ч; х₂=95м³/ч; х₃=100м³/ч; х₄=103м³/ч; х₅=99м³/ч; х₆=98м³/ч

будет

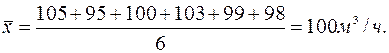
Необходимо обратить внимание на то, что выражение (2.2) справедливо только в том случае, если отдельные замеры… 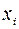… обладают одинаковой вероятностью. В противном случае оценка определяется по выражению

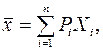(2.3)

где … 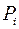… - вероятность замера.

Пример. Определить оценку для математического ожидания производительности гидромонитора по двум замерам:

- монитор работал 50 минут. За это время было отбито 20 тонн угля;

- монитор работал 10 минут и отбил 10 тонн угля.

В первом случае производительность составила … 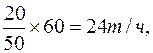…. а во втором … …

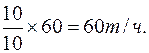Определим математическое ожидание по формуле (2.2)

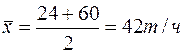
Полученный результат является ошибочным, т.к. вероятность работы с производительностью 24т/ч значительно больше, чем с производительностью 60т/ч. Правильное значение производительности можно найти по выражению (2.3)

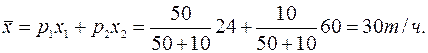
Для определения оценки генерального среднеквадратического отклонения первоначально находится дисперсия выборки

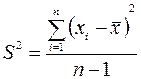(2.4)

В соответствии с ГОСТ 11004-74 оценкой для среднеквадратического отклонения генеральной совокупности … 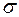…. является

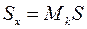(2.5)

где …… .;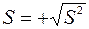

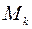… … - коэффициент, определяемый по табл. 2.2 в зависимости от числа степеней свободы … .. .

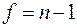Таблица 2.2

Значение коэффициента… ….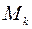

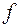
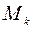
.	1.253	1.128	1.085	1.064	1.051	1.042	1.036	1.032	1.028	1.025

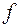
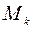
	1.004

Пример.Определить оценку для среднеквадратического отклонения подачи насоса по результатам шести замеров …x₁=105м³/ч;…х₂=95м³/ч;…х₃=100м³/ч;…х₄=103м³/ч;…х₅=99м³/ч;… х₆=98м³/ч .

Ранее было установлено, что … 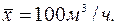… Тогда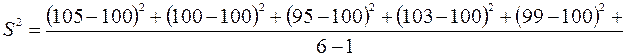

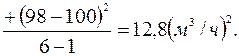
Из табл. 2.2 для …f=6-1=5… значение …M_k=1,051. .Следовательно,

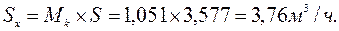
Полученное значение …S_х… является оценкой среднеквадратической абсолютной ошибки отдельного опыта.

Мерой точности среднего результата всех опытов является

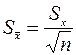(2.6)

В нашем примере

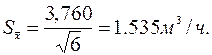
Из выражения (2.6) следует, что математическое ожидание в принципе можно определить с высокой точностью даже не особенно точным прибором. Но при этом необходимо выполнить большое число независимых измерений. Рациональнее для улучшения результата использовать более точные приборы с меньшим значением…S_х .