Методика определения безразмерных комбинаций

ПОДОБИЕ ОБЪЕКТОВ

Результаты данного эксперимента можно распространить лишь на подобные объекты. Два объекта или явления подобны / 1, 2, 3, 4 /, если по известным характеристикам одного можно получить характеристики другого простым пересчетом. Для таких объектов характерно равенство критериев подобия – безразмерных величин, составленных из размерных физических параметров, описывающих процессы в исследуемых объектах.

КРИТЕРИИ ПОДОБИЯ

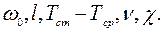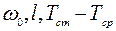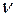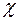Числа Рейнольдса, Пекле, Прандтля и др. содержат величины Первые три из них связаны с масштабом скоростей, размеров и температур и могут иметь любые, независящие одно от другого значения, определяемые исключительно граничными условиями; величины являются, таким образом, по отношению к уравнениям течения произвольными; и рассматриваются как параметры, характеризующие физические свойства жидкости. Величины 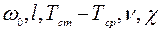называют характеристическими, т.к. определяют условия, в которых происходит движение жидкости.

Безразмерные комплексы, составленные из произвольно задаваемых величин (связанных через граничные условия с масштабами скоростей, геометрических размеров и температур) и физических свойств жидкости, т. е. включающие лишь характеристические величины, называют определяющими критериями. К ним относятся, в частност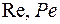и, и 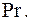Любые другие безразмерные комплексы, характеризующие течение жидкости, - функции определяющих подобие критериев.

Критерии подобия определяют относительное влияние как действующих в потоке сил, так и происходящих в потоке процессов переноса (напомним, что при течении вязкой теплопроводящей жидкости имеют место перенос импульса вследствие вязкости и перенос теплоты посредством теплопроводности).

Критерии подобия устанавливают динамическое или кинематическое подобие, суть которого состоит в том, что при одинаковом значении соответствующих (одного или нескольких) критериев отношения двух физических величин (например, сил) при одинаковой геометрии потоков имеют одно и тоже значение.

По численному значению критериев подобия можно оценить, насколько отличается поток вязкой и теплопроводящей жидкости от потока идеальной жидкости, и тем самым условно разделить поток на области, где действия вязкости или теплопроводности существенно различны.

Главнейшие критерии, используемые при описании течения вязкой и теплопроводящей жидкости, приводятся ниже.

Число Рейнольдса Re = 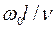- важнейший параметр гидродинамики; оно равняется соотношению силы инерции 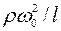к силе вязкости 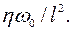При малых Re преобладают силы вязкости, при больших Re – силы инерции (в последнем случае влияние вязкости сказывается лишь в узкой области вблизи границ твердого тела, т.е. в пограничном слое).

Число Маха Ма = 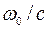является мерой сжимаемости газа при больших скоростях течения. При достаточно малых значениях Ма изменение плотности газа настолько мало, что газ можно рассматривать как несжимаемую жидкость. При Ма > 1 поток газа существенно отличается от потока газа при Ма < 1; в сверхзвуковом потоке газа возможно образование ударных волн, в дозвуковом потоке ударные волны никогда не образуются.

Равным образом существенные различия имеют трансзвуковой (Ма 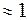) и гиперзвуковой (Ма >> 1). Из этого видно, что Ма – один из важнейших параметров газодинамики.

Число Прандтля 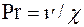характеризует относительное влияние теплопроводности вязкости на жидкость. Оно определяется только физическими свойствами жидкости и не зависит от таких условий течения, как скорость и геометрические размеры.

Число Нуссельта 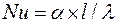равняется отношению полного теплового потока 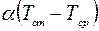к тепловому потоку, возникающему вследствие теплопроводности 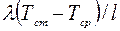, и , следовательно, выражает результирующий эффект влияния течения на теплообмен. Этим число Нуссельта отличается от других параметров подобия, которые выражают не результирующий, а частные эффекты.

Число Эйлера 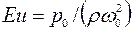представляет собой удвоенное отношение давления жидкости 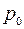к динамическому давлению 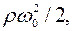обусловленному конечным значением скорости жидкости.

В соответствии с теорией подобия, при проведении эксперимента, необходимо измерять все величины, которые входят в состав критериев. Обрабатывать результаты следует в виде зависимостей между критериями подобия. Только в этом случае можно распространять результаты данного эксперимента на другие объекты. Существует два способа определения критериев: при помощи анализа размерностей и по уравнениям процесса.

1.1. 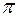– теорема и ее следствия.

В соответствии с 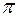- теоремой, если процесс в объекте характеризуется n фундаментальными величинами, для выражения размерностей которых используется k основных единиц, то его (процесс) можно описать n-k безразмерными комбинациями, составленными из этих величин.

Из теоремы следует два важных для практики вывода.

Первый. Уравнения, описывающие физические процессы, могут быть выражены уравнениями связи между безразмерными комбинациями – критериями подобия. Последние уравнения будут справедливы для всех подобных объектов.

Второй. Число безразмерных переменных меньше числа размерных на число основных единиц. Речь, таким образом, идет о снижении числа переменных, описывающих процесс. Это уменьшает объем экспериментальных исследований и делает результаты более наглядными.

Предположим, что процесс описывается n=5 физическим величинам.

Одна из них выходная – параметр и четыре входных - факторы. Мы решили экспериментальным путем установить связь между выходной и входными величинами, не переходя к безразмерным комбинациям. Предположим также, что при постановке опытов каждый фактор фиксируется на пяти уровнях. Тогда для перебора всех возможных сочетаний необходимо число опытов, равное сложности объекта, будет составлять C = 5⁴ = 625.

Посмотрим, что даст переход к безразмерным комбинациям. Предположим, что число основных единиц k = 3 (это очень часто встречающийся случай). В условиях рассматриваемого примера, в соответствии с 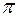- теоремой, после перехода к безразмерным комбинациям останется n – k = 5-3 = 2 безразмерных переменных. Одна из них – безразмерный параметр и вторая – обобщенный безразмерный фактор. Для одинаково достоверных с рассмотренным выше случаем теперь достаточно будет поставить всего пять опытов, т.е. в 125 раз меньше, чем раньше.

В последнем случае резко улучшается наглядность экспериментальной информации. Мы получим график зависимости одной выходной величины от одной входной.

Методика определения безразмерных комбинаций

Решение этой задачи состоит из трех этапов. На первом выбираются фундаментальные переменные. Обычно в выборе выходной переменной осложнений не бывает. Как правило, мы знаем, что необходимо определить. Входной фундаментальной переменной является любая величина, оказывающая влияние на выходную и способная изменяться независимо от других. Для правильного выбора фундаментальных переменных необходимо глубокое проникновение в существо исследуемого объекта. Часто это требует не только изучения априорной информации, но и постановки предварительного эксперимента. Если после выбора фундаментальных переменных система безразмерных комбинаций не получается, то необходимо возвратиться к анализу объекта.

На втором этапе выбирается система основных единиц для выражения размерностей фундаментальных переменных. При изучении гидравлических и механических процессов в большинстве случаев можно принять в качестве основных единиц массу (М), длину (L), и время (Т).

На третьем, заключительном этапе, на базе теории размерностей определяются безразмерные комбинации.