Регрессионный анализ
Целью его является установление аналитической зависимости между выходной и входными величинами. При проведении исследований инженеру-электромеханику часто приходится решать подобные задачи. Известно, что в общем случае зависимость между величинами может быть представлена таблично, графически и аналитически. Первый способ облегчает определение выходной величины для приведенных в таблице значений входных; графический - создает наглядность представления. Аналитическая зависимость позволяет исследовать функцию методами математического анализа, т.е. определить значения максимума, точек перегиба и т.д. Без аналитической зависимости осложняется исследование систем регулирования, проведение расчетов на ЭВМ. Аналитическая зависимость является наиболее универсальной. Из нее просто получается табличная и графическая. Если входных величин более двух, то табличное и графическое представления теряют наглядность.
В регрессионном анализе в отличие от корреляционного только выходные величины являются случайными. Входные должны быть неслучайными и некоррелированными между собой.
Необходимо иметь в виду, что, если теоретические формулы, полученные на основе знания законов того или иного процесса, могут быть использованы при произвольных значениях аргумента, то эмпирические, полученные путем обработки данных замеров, являются приближенными и могут применяться лишь в четко определенных условиях и в строго ограниченных пределах аргумента. Один и тот же процесс может быть описан несколькими эмпирическими формулами.
Задача получения аналитической зависимости включает три этапа: выбор уравнения регрессии; определение коэффициентов уравнения; проверка соответствия установленной зависимости экспериментальному материалу /5,6,7,9/.
Первый этап является неформализованной процедурой. Здесь многое зависит от опыта исследователя. Уже отмечалось. что один и тот же процесс может быть описан различными эмпирическими зависимостями. на практике при выборе вида уравнения обычно руководствуются следующим. По данным эксперимента первоначально строят «пробную» графическую зависимость. Ее сравнивают с различными кривыми, уравнения которых известны и останавливаются на наиболее вероятной.
Для получения наглядной картины и облегчения выбора правильной аналитической зависимости, график следует строить в прямоугольной системе координат первоначально с равномерными шкалами на осях.
Масштабы на осях координат определяются по следующим выражениям:
 и
и 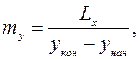
где 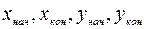 - начальные и конечные значения аргумента и функции в условиях эксперимента;
- начальные и конечные значения аргумента и функции в условиях эксперимента;
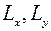 – длины шкал.
– длины шкал.
Длины шкал определяются условиями размеров чертежа. При этом масштабы должны быть округленными.
Выбирая 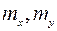 , следует иметь в виду, что их уменьшение ведет к снижению точности обработки. Масштабы следует принимать такими, чтобы ошибка измерения на чертеже изображалась отрезком не менее 1мм. Чрезмерное увлечение масштабом ведет к подчеркиванию случайных отклонений опытных точек, что затрудняет выбор правильной аналитической зависимости. Соотношение между
, следует иметь в виду, что их уменьшение ведет к снижению точности обработки. Масштабы следует принимать такими, чтобы ошибка измерения на чертеже изображалась отрезком не менее 1мм. Чрезмерное увлечение масштабом ведет к подчеркиванию случайных отклонений опытных точек, что затрудняет выбор правильной аналитической зависимости. Соотношение между  и
и 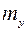 должно обеспечивать примерно одинаковый наклон экспериментальной линии к осям координат
должно обеспечивать примерно одинаковый наклон экспериментальной линии к осям координат
Если график не имеет максимума, минимума или других особенностей, то для получения приемлемой точности и снижения объема вычислений при построении искомой зависимости достаточно ограничится 4 – 6 и максимум 10 точками.
При наличии в исходном экспериментальном материале большого числа точек следует проводить их группировку.
Если в результате построений окажется, что некоторые точки существенно отклонялись от общей зависимости, то следует проверить вычисления для них, а при необходимости повторить эксперимент.
Проведенная по экспериментальным данным «пробная « кривая должна быть плавной, проходить возможно ближе ко всем точкам. Ее следование за каждой точкой подчеркивает случайные изменения и искажает искомую зависимость.
В ряде случаев может оказаться, что еще до обработки экспериментальных данных известна, пусть даже примерная, теория исследуемого процесса. В этом случае функциональная зависимость, определяемая этой теорией. может дать представление о возможном виде эмпирической формулы.
Например, известно, что теоретическая напорная характеристика турбомашины при постоянной частоте вращения является прямой линией. Известно также, что потери напора в турбомашине пропорциональны квадрату расхода. В этих условиях при выборе формулы для описания экспериментальной напорной характеристики наиболее целесообразной является ориентация на квадратичные зависимости.
При выборе формулы нет необходимости ориентироваться на сложные зависимости. Дело в том, что, с одной стороны, любая полученная в результате математической обработки экспериментальных данных формула будет только приближенно отражать существо процесса. Ценность формулы определяется не сложностью, а той ошибкой, какую мы допускаем при ее применении. С другой стороны, для сложных зависимостей резко возрастает объем вычисленных и других операций для определения параметров, характеризующих их.
При рассмотрении вопроса определения коэффициентов уравнения регрессии считаем необходимым первоначально обратить внимание на следующее. При выбранном виде уравнения эта задача на ЭВМ решается по стандартным программам. Поэтому нет необходимости приводить общие выкладки, а можно ограничиться вскрытием сущности процедуры определения коэффициентов на предельно простом примере – на примере линейной зависимости.
Известно, что линейная зависимость описывается уравнением
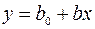 (2.19)
(2.19)
где у – искомая функция (выходная величина);
х – аргумент (входная величина);
во, в - коэффициенты регрессии, постоянные величины.
Наиболее достоверные значения коэффициентов получаются при использовании для их определения метода наименьших квадратов.
Процедура проверки соответствия установленной зависимости экспериментальному материалу (проверка адекватности) включает три этапа.
Первый. Ищется остаточная дисперсия или дисперсия адекватности
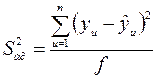 (2.26)
(2.26)
Здесь yu - экспериментальное значение выходной величины для соответствующего значения xu ;
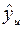 - рассчитанное по уравнению регрессии значение функции для данного xu ;
- рассчитанное по уравнению регрессии значение функции для данного xu ;
n – число опытов ;
f = n-l – число степеней свободы ;
l – число коэффициентов в уравнении регрессии .
Уже по  можно судить о степени соответствия уравнения экспериментальному материалу. Ведь
можно судить о степени соответствия уравнения экспериментальному материалу. Ведь  - среднеквадратическое отклонение экспериментальных точек от значений, полученных по уравнению.
- среднеквадратическое отклонение экспериментальных точек от значений, полученных по уравнению.
Второй. Определяется дисперсия воспроизводимости
На каждом уровне аргумента xu проводится несколько параллельных опытов, ищутся дисперсии для каждой группы экспериментов, проверяется их однородность и затем определяется средневзвешенная дисперсия 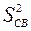 (см. раздел 2.6). Она и является дисперсией воспроизводимости
(см. раздел 2.6). Она и является дисперсией воспроизводимости 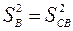 .
.
Если параллельные опыты не проводятся, то в качестве средневзвешенной дисперсии принимается
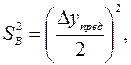
где 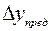 – предельная абсолютная ошибка в определении входной величины.
– предельная абсолютная ошибка в определении входной величины.
Ранее было показано, что с доверительной вероятностью 0,955 можно считать предельную ошибку, равной 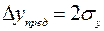 .
.
Третий. Поверяется однородность дисперсий адекватности и воспроизводимости.
Если расчетное значение критерия Фишера окажется меньше табличного, то полученное уравнение регрессии адекватно эксперименту
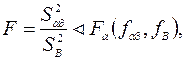 (2.27)
(2.27)
где 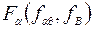 – берется из таблиц с учетом принятого уровня значимости для соответствующих степеней свободы
– берется из таблиц с учетом принятого уровня значимости для соответствующих степеней свободы 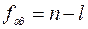 и
и 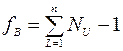 .
.
Здесь Nu - число параллельных опытов на каждом уровне аргумента.
Пример.В результате испытаний центробежного насоса установлено, что создаваемые им напоры при соответствующих подачах определяются значениями, приведенными в табл. 2.5.
Таблица 2.5
Зависимость напора насоса от подачи
| Q , м3/час | ||||||
| Н, м вод. ст. |
Известно также, что напор определяется с точностью  м вод. ст.
м вод. ст.
Требуется установить аналитическую зависимость напора Н от подачи Q. Для выбора вида формулы изобразим табличные данные графически.
Наименьшее значение подачи при эксперименте 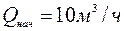 мало отличается от нуля в сравнении с наибольшим.
мало отличается от нуля в сравнении с наибольшим. 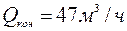 . Поэтому градуировку шкалы подачи начнем с нулевого значения. Примем длину
. Поэтому градуировку шкалы подачи начнем с нулевого значения. Примем длину 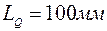 Тогда
Тогда

Округлим масштаб до 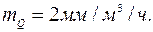
Для напора градуировку шкалы начнем с 50м. вод.ст. Примем длину шкалы LH = 100мм.
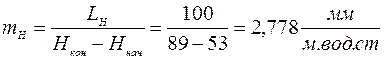
Пусть 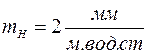 . Тогда предельная ошибка в определении напора
. Тогда предельная ошибка в определении напора 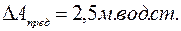 на графике будет изображаться отрезком 5мм
на графике будет изображаться отрезком 5мм
При 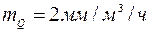 и
и 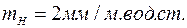 экспериментальная кривая окажется примерно одинаково наклоненной к осям координат. экспериментальные данные изображены на рис. 2.6. Рисунок дает основание предполагать между напором и подачей линейную зависимость.
экспериментальная кривая окажется примерно одинаково наклоненной к осям координат. экспериментальные данные изображены на рис. 2.6. Рисунок дает основание предполагать между напором и подачей линейную зависимость.
Предположим, что
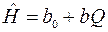
Для определения коэффициентов по данным табл.2.5 найдем 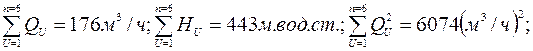
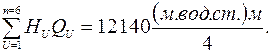
После подстановки этих данных в уравнения (2.22) и (2.23), получим
 ;
;
12140-176b0-6074b=0
Решив эту систему уравнений, получим 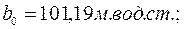 ,
,

Таким образом,
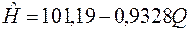 (2.28)
(2.28)

Рис. 2.6. Экспериментальная напорная характеристика
центробежного насоса
Эта зависимость на рис. 2.6 изображена пунктирной линией.
Проверим адекватность полученного уравнения регрессии. Данные для расчета дисперсии адекватности сведены в табл.2.6.
Таблица 2.6
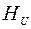
| 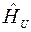
| 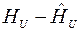
| 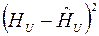
| 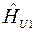
| 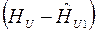
| 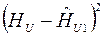
|
| 91.86 | - 2.862 | 8.191 | 88.78 | 0.22 | 0.0484 | |
| 82.53 | 0.466 | 0.2172 | 83.86 | - 0.86 | 0.7396 | |
| 76.94 | 1.063 | 1.1305 | 79.34 | - 1.334 | 1.779 | |
| 4.592 | 21.09 | 72.56 | 2.106 | 5.952 | ||
| 63.88 | 1.122 | 1.259 | 64.18 | 0.82 | 0.6724 | |
| 57.3484 | -4.3484 | 18.91 | 54.19 | - 1.192 | 1.422 | |
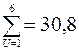 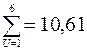
|
Дисперсию  определим по выражению (2.26)
определим по выражению (2.26)
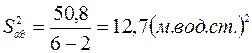
В соответствии с изложенным выше дисперсия воспроизводимости в данном случае
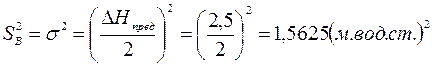
Расчетное значение F - критерия
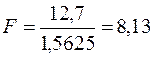
Для уровня значимости 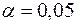 , а также чисел степеней свободы
, а также чисел степеней свободы 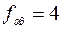 и
и 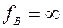 табличное значение критерия
табличное значение критерия 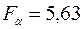 . Так как расчетное значение больше табличного, то уравнение (2.28) не адекватно экспериментальному материалу.
. Так как расчетное значение больше табличного, то уравнение (2.28) не адекватно экспериментальному материалу.
Учитывая , что процессы протекающие в насосе, дают основание предполагать между напором и подачей квадратическую зависимость, найдем коэффициенты уравнения вида
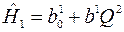
По данным эксперимента определим в дополнение к известным
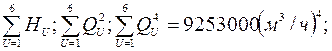
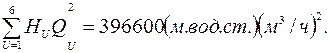
Подставив в уравнение (2.24) и (2.25) значение соответствующих величин, получим
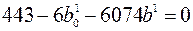
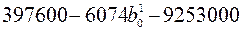 b1=0
b1=0
Решение этой системы уравнений дает следующие результаты:
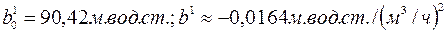
Таким образом,
 Q2 (2.29)
Q2 (2.29)
На рис.2.6 последняя зависимость изображена сплошной кривой.
Данные для определения дисперсии адекватности приведены в табл.2.6.
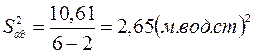
Расчетное значение критерия Фишера
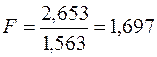
Так как оно меньше табличного 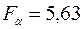 , то полученная нами зависимость (2.29) адекватна эксперименту.
, то полученная нами зависимость (2.29) адекватна эксперименту.
Дата добавления: 2016-05-25; просмотров: 875;
