Проверка однородности дисперсий

Допустим, требуется экспериментально установить связь между параметром объекта У и фактором Х. Для этого на каждом контрольном уровне фактора для повышения точности результатов будем проводить несколько параллельных замеров параметра. В результате эксперимента получим ряд выборок. Каждая из них характеризуется своим математическим ожиданием и своей дисперсией. В общем случае

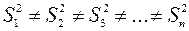
Наиболее распространенным методом проверки однородности дисперсий является проверка с помощью критерия Фишера /6/ .

Этот критерий ( F – критерий ) представляет отношение большей дисперсии к меньшей

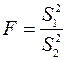(2.11)

где .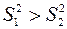

Расчетное значение критерия сравнивают с критическим табличным, определяемым для принятого уровня значимости и соответствующих дисперсиям 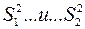степеней свободы f₁ f₂ .Значение F – критерия при пятипроцентном уровне значимости приведены в табл. 2.4. Необходимо иметь в виду, что

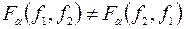
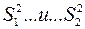Если расчетное , то дисперсии однородны и вместо можно пользоваться средневзвешенным значением

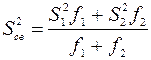(2.12)

Когда мы располагаем не двумя, а набором U дисперсий, то с помощью F – критерия проверяется однородность наименьшей и наибольшей. Если различие между ними окажется незначимым, то другие дисперсии тем более будут однородными. В этом случае для всей совокупности средневзвешенная дисперсия определяется из выражения

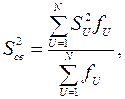
(2.13)

где N – число дисперсий.

Таблица 2.4

Значение F – критерия при уровне значимости 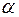= 0,05

Число степеней свободы
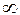
	161.0	200.0	216.0	225.0	230.0	234.0	242.0	248.0	252.0	253.0	254.0
	18.51	19.00	19.16	19.25	19.30	19.39	19.39	19.44	19.47	19.49	19.50
	10.13	9.55	9.28	9.12	9.01	8.94	8.78	8.66	8.58	8.56	8.53
	7.71	6.94	6.59	6.39	6.26	6.16	5.96	5.80	5.70	5.66	5.63
	6.61	5.79	5.41	5.19	5.05	4.95	4.74	4.56	4.44	4.40	4.36
	5.99	5.14	4.76	4.53	4.39	4.28	4.06	3.87	3.75	3.71	3.67
	5.32	4.46	4.07	3.84	3.69	3.58	3.34	3.15	3.03	2.98	2.93
	4.96	4.10	3.71	3.48	3.33	3.22	2.97	2.77	2.64	2.59	2.54
	4.35	3.49	3.10	2.87	2.71	2.60	2.35	2.18	1.96	1.90	1.84
	4.08	3.23	2.83	2.61	2.45	2.34	2.07	1.84	1.66	1.59	1.51
	4.08	3.23	2.83	2.61	2.45	2.34	2.07	1.84	1.66	1.59	1.51
∞	3.94	3.09	2.70	2.46	2.30	2.19	1.92	1.68	1.48	1.39	1.28