Сравнение двух выборочных средних.
Пусть усовершенствована какая-либо машина, например, выемочная. Для оценки полезности сделанного поставлен сравнительный эксперимент: проведен ряд замеров производительности до и после реконструкции. В результате эксперимента получены две выборки. Первая – число замеров 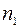 ,математическое ожидание
,математическое ожидание 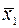 , и дисперсия
, и дисперсия 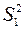 . Вторая – число опытов
. Вторая – число опытов 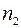 , математическое ожидание
, математическое ожидание 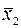 , дисперсия выборки
, дисперсия выборки 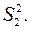 При этом
При этом
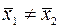
Ставиться вопрос: можно ли утверждать, что различие между 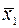 и
и 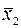 значимо? Иными словами, можно ли утверждать, что реконструкция дала положительные результаты.
значимо? Иными словами, можно ли утверждать, что реконструкция дала положительные результаты.
Обозначим
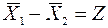 (2.14)
(2.14)
Z будет значимой величиной, если выйдет за пределы доверительного интервала

Предположим, что различие между … 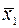 … и …
… и … 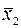 …незначимо, т.е. предположим …
…незначимо, т.е. предположим …  ….
….
Тогда доверительный интервал
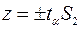
В разделе 2.4. показано, что
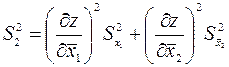
С учетом выражения (2.14) следует
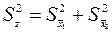
Так как 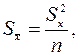 то
то 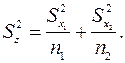
Если 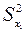 и
и  однородны, а только в этом случае можно сравнивать
однородны, а только в этом случае можно сравнивать 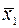 и
и 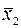 , то
, то
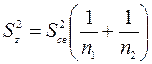 или
или 
Таким образом, доверительный интервал
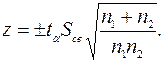 (2.15)
(2.15)
Критерий  берется для соответствующего уровня значимости и числа степеней свободы
берется для соответствующего уровня значимости и числа степеней свободы 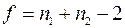 .
.
Пример.В одинаковых условиях проведены испытания двух выемочных комбайнов. Получены следующие равновероятные данные для производительности:
-.до реконструкции: 39; 34; 58; 45; 34; 38 т/ч
- после реконструкции: 40; 47; 50; 53; 49; 45 т/ч
Найдем оценки математических ожиданий
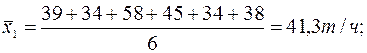
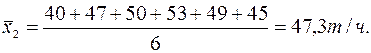
На первый взгляд кажется, что реконструкция привела к существенному увеличению производительности машины - на 14,5% . Проверим достоверность этого.
Используя выражение (2.4), найдем оценки дисперсий
 и
и 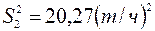
В соответствии с выражением (2.5)
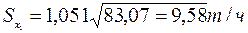 и
и 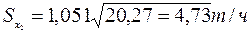
Для проверки однородности параллельных опытов в выборках по выражению (2.9) определим доверительные интервалы
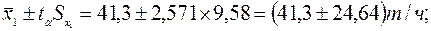
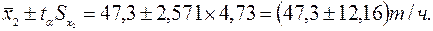
Таким образом, каждая из выборок состоит из однородных результатов.
Проверим однородность дисперсий. Определим расчетное значение критерия Фишера

Табличное значение F - критерия при уровне значимости 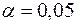 и
и 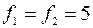 составляет 5,05. Следовательно, дисперсии однородны.
составляет 5,05. Следовательно, дисперсии однородны.
В соответствии с выражением (2.12) определим

По уравнению (2.15) доверительный интервал
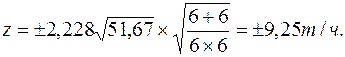
Так как этот интервал включает различия между математическими ожиданиями
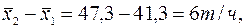
то с вероятностью 0,95 экспериментальный материал не дает оснований утверждать, что реконструкция комбайна привела к значимому увеличению производительности.
Дата добавления: 2016-05-25; просмотров: 574;
