Давление жидкости на криволинейную стенку

Рассмотрим теперь случай, когда участок поверхности, на который рассматривается действие жидкости, не является плоским (рис. 2.15). Давление на свободной поверхности жидкости примем равным атмосферному давлению. Вычислим сначала главный вектор сил давления.

Согласно формулам (2.18) и (2.17), имеем:

,

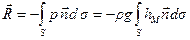или в проекциях на оси координат (ось OZ направлена вниз, плоскость XOY совпадает со свободной поверхностью жидкости):

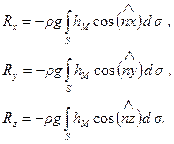(2.32)

Поскольку справедливы соотношения

,

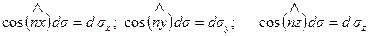где 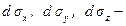площади проекций элементарной площадки 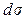на плоскости, перпендикулярные соответствующим осям координат (рис. 2.17), то формулы (2.32) приобретают вид

,

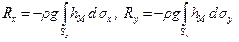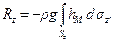(2.33)

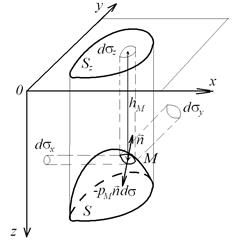
Рис. 2.17.Расчет сил давления жидкости

на криволинейную стенку

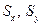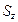Положим, что и — площади проекций криволинейной стенки на плоскости перпендикулярные координатным осям ( 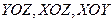, соответственно). Необходимо, однако, отметить, что эти площади суммируются алгебраически, т.е. учитывается знак проекции; знак проекции зависит от того, положительный или отрицательный косинус угла проецирования участка поверхности на соответствующую координатную плоскость. Так, например, для замкнутой поверхности все три проекции равны нулю.

Интегралы, стоящие в правых частях формул (2.33), связаны с координатами центров тяжести проекций стенки на координатные плоскости следующими соотношениями:

а)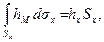

где 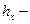глубина от свободной поверхности центра тяжести проекции стенки 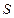на плоскость, перпендикулярную оси ОХ, а 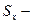алгебраическая площадь этой проекции;

б)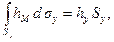

где 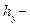глубина от свободной поверхности центра тяжести проекции стенки на плоскость, перпендикулярную оси 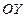, a 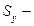алгебраическая площадь этой проекции;

в)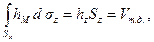

где 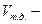объем тела давления, т.е. объем тела, заключенного между поверхностью 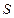, ее проекцией на свободную поверхность и вертикальными проектирующими образующими.

Собирая полученные результаты воедино, получаем:

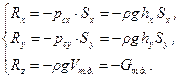(2.34)

Здесь 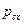и 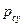— избыточные давления на глубине центра тяжести проекци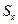й и 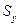, соответственно; 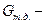вес жидкости в объме тела давления.

Таким образом, можно сделать следующие выводы:

а) Горизонтальные составляющие главного вектора сил давления на криволинейную стенку равны произведениям избыточных давлений в центрах тяжести проекций этой поверхности на вертикальные плоскости на алгебраические площади этих проекций;

б) Вертикальная составляющая главного вектора сил давления равна весу жидкости в объеме тела давления;

в) Величина 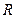главного вектора 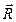сил давления находится по формуле:

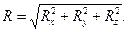(2.35)

Пример. Найти силу давления на полусферическую стенку открытого сосуда, заполненного водой. Радиус сферы 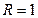м, 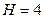м (рис. 2.18).

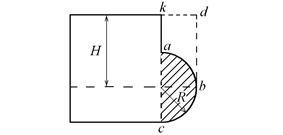
Рис. 2.18.Пример расчета силы давления жидкости

на криволинейную стенку

Решение. Для вычисления горизонтальной составляющей 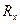силы давления (ось 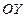направлена перпендикулярно к площади чертежа) используем формулы (2.34):

^,

^.

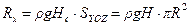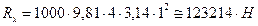Чтобы найти вертикальную составляющую 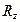силы давления, разобьем поверхность полусферы на две равные части – верхнюю ab и нижнюю bc, и вычислим вертикальные составляющие сил давления для каждой из этих частей.

На часть ab стенки действует сила давления, вертикальная составляющая которой равна весу жидкости в объеме abdk; эта сила направлена вверх. На часть bc стенки действует сила давления, вертикальная составляющая которой равна весу жидкости в объеме bckd; эта сила направлена вниз. Вертикальная составляющая силы давления для всей полусферы abc равна разности полученных сил:

,

.

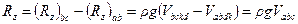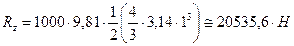Таким образом, 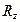для полусферической стенки равна весу жидкости в объеме полусферы и направлена вниз.

Ответ: 20535,6 Н ( 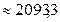кГс).