Гидравлический пресс
Гидравлический пресс представляет собой простейший механизм, с помощью которого можно получить выигрыш в силе, т.е. с помощью меньшей по величине силы получить большую силу. Принципиальная схема такого пресса показана на рис. 2.8.
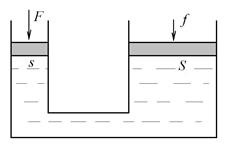
Рис. 2.8. Принцип дейстия гидравлического пресса
Пресс состоит из двух цилиндров, в каждом из которых под поршнем находится несжимаемая (или слабо сжимаемая) жидкость, причем площадь  поршня в левом цилиндре меньше площади
поршня в левом цилиндре меньше площади 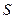 в правом цилиндре; пространства под поршнями образует сообщающиеся сосуды.
в правом цилиндре; пространства под поршнями образует сообщающиеся сосуды.
Если к левому поршню приложить силу  , то давление под этим поршнем изменится на величину
, то давление под этим поршнем изменится на величину  . Поскольку из закона Паскаля следует, что на такую же величину должно измениться давление под правым поршнем, то для удержания этого поршня в равновесии к нему необходимо приложить силу
. Поскольку из закона Паскаля следует, что на такую же величину должно измениться давление под правым поршнем, то для удержания этого поршня в равновесии к нему необходимо приложить силу  , т. е. должно выполняться равенство
, т. е. должно выполняться равенство
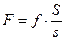 .
.
Поскольку 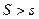 , то сила
, то сила 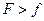 .
.
Таким образом, приложив относительно небольшую силу  к поршню с меньшей площадью, мы получим увеличенную силу
к поршню с меньшей площадью, мы получим увеличенную силу  , действующую на поршень с большей площадью, причем сила увеличивается в
, действующую на поршень с большей площадью, причем сила увеличивается в 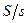 раз. Если поршни имею круглые сечения¸ то увеличение силы равно отношению квадратов диаметров этих сечений.
раз. Если поршни имею круглые сечения¸ то увеличение силы равно отношению квадратов диаметров этих сечений.
Заметим, однако, что, как и все прочие механизмы, гидравлический пресс дает выигрыш в силе, но не в работе. Поскольку перемещение 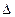 поршня в цилиндре с большей площадью меньше перемещения
поршня в цилиндре с большей площадью меньше перемещения 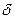 поршня в цилиндре с меньшей площадью, то работы
поршня в цилиндре с меньшей площадью, то работы 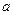 и
и 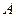 , производимые обеими силами, равны по величине. Действительно, из равенства изменения объемов жидкости в полостях пресса следует, что
, производимые обеими силами, равны по величине. Действительно, из равенства изменения объемов жидкости в полостях пресса следует, что 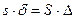 , т.е.
, т.е. 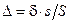 , поэтому справедливы следующие равенства:
, поэтому справедливы следующие равенства:
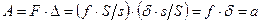 .
.
Иными словами, работы обеих сил равны по величине.
Пример 1. Определить абсолютное давление на дне резервуара, в котором находиться бензин (плотность  =730 кг/м3), если уровень жидкости в резервуаре равен H=16 м, а давление насыщенных паров над плавающим понтоном составляет p0=1,03 ат (рис. 2.9).
=730 кг/м3), если уровень жидкости в резервуаре равен H=16 м, а давление насыщенных паров над плавающим понтоном составляет p0=1,03 ат (рис. 2.9).
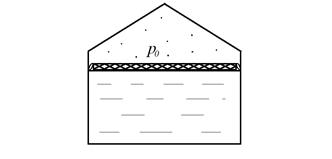
Рис. 2.9.Вертикальный резервуар с понтоном
Решение. Давление в точках дна резервуара  определяется формулой
определяется формулой
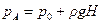 .
.
Подставляя в эту формулу числовые данные, находим
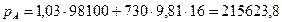
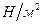
Ответ:  Па.
Па.
Пример 2. Определить величину вакуума над поверхностью жидкости в перевернутом стакане, если уровень воды в этом стакане h = 20 см (рис. 2.10).
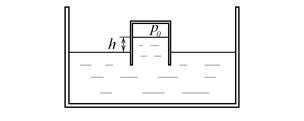
Рис. 2.10. Вакуум в перевернутом стакане
Решение. Пусть 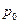 – абсолютное давление над жидкостью в стакане, тогда
– абсолютное давление над жидкостью в стакане, тогда
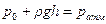 .
.
Поскольку вакууметрическое давление определяется формулой
 ,
,
то
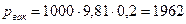
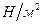 = 1962 Па.
= 1962 Па.
Ответ: 1962 Па.
Дата добавления: 2016-05-16; просмотров: 1254;
