Распределение давления в покоящейся жидкости

Найдем распределение давления в однородной несжимаемой жидкости ( 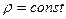), находящейся в состоянии равновесия под действием силы тяжести. Если плоскость 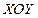расположить горизонтально, а ось 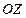направить вертикально вверх, то единственной массовой силой будет сила тяжести с проекциями напряжения

,

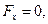
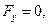
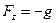где 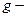ускорение силы тяжести.

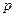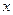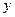Поскольку в горизонтальном направлении на частицы жидкости массовые силы не действует, то это означает, что давление не зависит от координат и . Этот же вывод следует из уравнений равновесия (2.12):

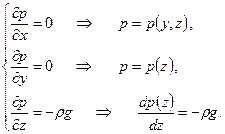
Из последнего уравнения системы следует, что давление в покоящейся жидкости с постоянной плотностью линейно увеличивается с глубиной:

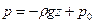, (2.14)

где 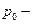постоянная интегрирования.

Поверхность, давление на которой постоянно, называется изобарической поверхностью. Из уравнения 2.14 видно, что для однородной несжимаемой жидкости, находящейся в состоянии равновесия под действием силы тяжести, уравнением поверхности является 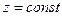, т. е. горизонтальная плоскость. Изобарическую поверхность, давление на которой равно атмосферному, называют пьезометрической.

Если жидкость имеет свободную поверхность, на которой давление постоянное (например, если жидкость, находящаяся в резервуаре, граничит по этой поверхности с газом, причем давление на поверхности контакта можно считать постоянным), то из (2.14) следует, что уравнение этой поверхности есть 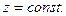, т.е. свободная поверхность является плоскостью. Принимая эту поверхность за 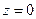, можно видеть, что 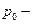это давление на свободной поверхности.

Обозначая глубину 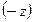горизонтального слоя жидкости под свободной поверхностью 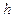, т.е. полагая 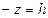, (рис. 2.3), имеем:

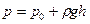. (2.15)

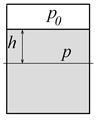
Рис. 2.3. Гидростатическое давление в сосуде

Формула (2.15), называемая формулой гидростатического распределения давления, читается так: столб жидкости высотой 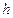создает в своем основании дополнительное давление .

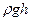Закон Паскаля

Если давление в какой-либо точке покоящейся несжимаемой жидкости изменить на некоторую величину, то на такую же величину изменится давление в любой другой точке жидкости. Это утверждение, читаемое как давление передается одинаково во все стороны, составляет сущность закона Паскаля.

Рассмотрим две точки А и В в покоящейся жидкости (рис. 2.4).

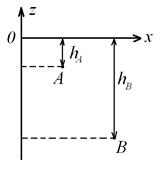
Рис. 2.4. К выводузакона Паскаля

Из уравнения (2.15) имеем:

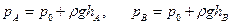
Отсюда следует, что давления и 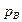связаны равенством

.

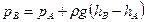Пусть теперь давление в точке А изменили на величину 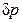, так что

,

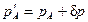тогда давление в точке В также изменится:

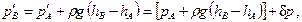
или

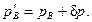
Таким образом, давление в точке В изменилось на ту же самую величину 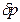, что и в точке 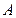, как и утверждает закон Паскаля.

В качестве наглядной иллюстрации этого закона укажем на всем известный опыт Торричелли с бочкой (рис. 2.5).

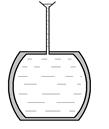
Рис. 2.5. Схема опыта Торичелли

Если сверху в бочку вставить длинную трубку и залить ее водой, то бочка разрыватся. Давление в точке, в которую подведена трубка, повышается; на ту же величину повышается давление и в остальных точках жидкости, и бочка разрывается.