Элементы поверхности тел, погруженных в жидкость

Формула (2.15) для распределения давления в покоящейся жидкости позволяет решить одну из фундаментальных задач гидростатики, дать ответ на вопрос о силовом действии со стороны жидкости на элементы поверхности тела, погруженного в жидкость.

Пусть криволинейный участок S (рис. 2.11) представляет элемент поверхности некоторого тела, погруженного в жидкость.

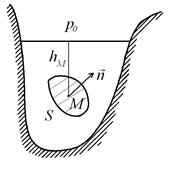
Рис. 2.11. Силы давления, действующие на элемент поверхности тела, погруженного в жидкость

Давление жидкости в точке М поверхности S за вычетом дополнительного давления столба воздуха на свободную поверхность 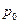, согласно (2.15) выражается равенством

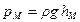, (2.17)

где 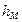— глубина точки М под свободной поверхностью.

Известно, что если некоторая система сил действует на твердое тело, то выбрав в этом теле некоторую точку О за полюс, можно все силы перенести в эту точку параллельным сдвигом, добавляя соответствующие пары сил. После этого оказывается, что система сил сводится к одной силе и к одной паре сил. Эта одна сила называется главным вектором сил давления жидкости на поверхность S. Его величина представляется интегралом

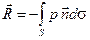, (2.18)

где интегрирование происходит по поверхности 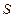. При переходе к другому полюсу 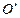главный вектор сил не изменяется.

Главный момент 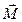сил давления жидкости на стенку 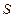определяется равенством

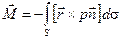, (2.19)

где 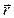— радиус-вектор произвольной точки поверхности 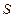пo отношению к точке О. При переходе от точки О к другому полюсу 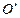величина главного момента изменяется.