Относительное равновесие жидкости в сосуде,

Рассмотрим открытый цилиндрический сосуд с жидкостью, вращающийся вокруг своей оси с постоянной угловой скоростью 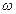(рис. 2.19).

Если систему отсчета связать с вращающимся цилиндром, то жидкость в такой системе будет находиться в относительном покое. Поскольку из массовых сил на жидкость действует только сила тяжести, то компоненты 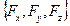имеют вид:

, , .

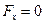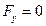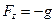Переносное ускорение 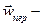это в данном случае центростремительное ускорение частиц, вращающихся по окружности радиуса :

,

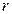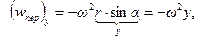
где 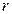- есть расстояние рассматриваемой точки от оси вращения: .

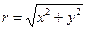Подставляя компоненты векторов 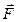и 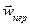в уравнения (2.36), записанные в виде полного дифференциала, получаем:

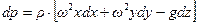. (2.37)

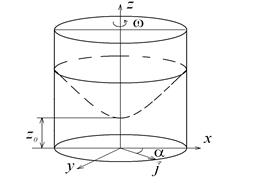
Рис. 2.19. Относительное равновесие жидкости

во вращающемся сосуде

Интегрируя (2.37), находим:

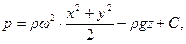(2.38)

где 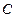- постоянная интегрирования. Постоянная интегрирования может быть найдена, если считать известным давление хотя бы в одной точке вращающейся жидкости. Например, если уровень 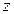жидкости на оси 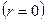цилиндра считать известным, а именно, 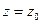, то давление 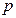в этой точке следует принять равным давлению 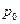на свободной поверхности жидкости:

.

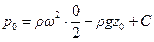Отсюда находим: 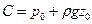. Подставляя 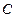в (2.38), получаем формулу для распределения давления:

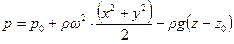(2.39)

или

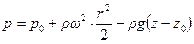. (2. )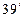

Используя (2.39), можно найти уравнение свободной поверхности жидкости во вращающемся сосуде. Поскольку во всех точках этой поверхности давление постоянное 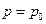, то уравнение этой поверхности имеет вид

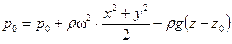
или

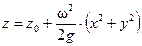. (2.40)

Уравнение (2.40) определяет в пространстве параболоид вращения, выпуклый вниз, с координатами вершины 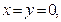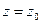, рис.2.19. Если вычислить объем жидкости, находящейся в сосуде под свободной поверхностью

,

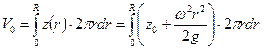где 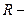радиус цилиндра, то получим зависимость координаты 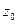вершины параболы от объема жидкости в сосуде и угловой скорости вращения:

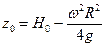, (2.41)

где 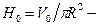глубина жидкости в цилиндре, если он не вращается. Из (2.41) следует, в частности, что при достаточно большой угловой скорости 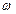вращения вершина параболы может коснуться дна, т.е. 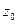сделаться равным 0. Такая картина имеет место, если угловая скорость 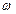вращения цилиндра определяется равенством

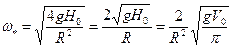. (2.42)

Если 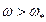, то некоторая круговая область дна цилиндра становится сухой, т.е. непокрытой жидкостью.

Другие поверхности равного давления в жидкости, вращающейся вместе с сосудом, на которых 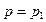> 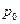, определяются, как это следует, из (2.39), уравнениями

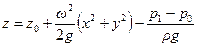, (2.43)

т.е. представляют собой параболоиды вращения, сдвинутые друг относительно друга вдоль вертикальной оси.