Взаиморастворимые жидкости в любых соотношениях.
Для идеальных растворов справедлив закон Рауля:
Парциальное давление каждого компонента, например, низкокипящего компонента А в паре 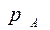 , пропорционально мольной доле
, пропорционально мольной доле 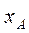 этого компонента в жидкости. При этом коэффициент пропорциональности равен давлению насыщенного пара
этого компонента в жидкости. При этом коэффициент пропорциональности равен давлению насыщенного пара 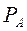 над жидкостью чистого компонента А при данной T°C.
над жидкостью чистого компонента А при данной T°C.
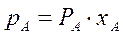 (3.1)
(3.1)
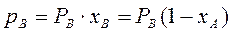 (3.2)
(3.2)
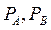 (большое) - давления насыщенных паров над чистыми жидкостями А и В.
(большое) - давления насыщенных паров над чистыми жидкостями А и В.
По первому закону Дальтона, общее давление пара над раствором P равно сумме парциальных давлений его компонентов:
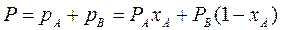 (3.3)
(3.3)
Тогда
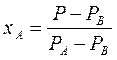 (3.4)
(3.4)
По второму закону Дальтона 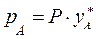 и тогда с учетом (3.1) получим:
и тогда с учетом (3.1) получим:
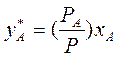 (3.5)
(3.5)
Попытаемся построить диаграмму T – x,y
По уравнению (3.4) 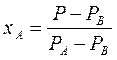 по известным
по известным 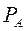 и
и 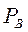 при заданной температуре кипения
при заданной температуре кипения 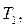 и
и 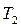 и т.д. находим
и т.д. находим 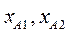 и т.д. Затем по уравнению (3.5) находим
и т.д. Затем по уравнению (3.5) находим 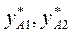 и т.д. По найденным точкам строим линию кипения жидкости и конденсации паров (рис 3.1).
и т.д. По найденным точкам строим линию кипения жидкости и конденсации паров (рис 3.1).

Рис.3.1 Фазовая диаграмма T – x, y.
Здесь линия 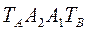 - отвечает фазе, находящейся при температуре кипения, а линия
- отвечает фазе, находящейся при температуре кипения, а линия 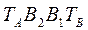 - конденсации.
- конденсации.
Любая точка лежащая выше этой линии конденсации, соответствует паровой фазе, пары являются перегретыми. Точка C характеризует систему, температура которой выше температуры кипения и ниже температуры конденсации паров этого же состава. Область между линиями 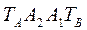 и
и 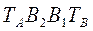 соответствует равновесным парожидкостным системам.
соответствует равновесным парожидкостным системам.
По уравнениям (3.3 - 3.5) можно получить уравнение линии равновесия:
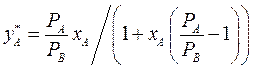 (3.6)
(3.6)
Уравнение получено для идеальных бинарных систем. Обозначим 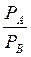 =α – относительная летучесть. Поскольку давления насыщенных паров
=α – относительная летучесть. Поскольку давления насыщенных паров 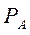 и
и 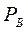 чистых компонентов А и В меняются в интервале температур
чистых компонентов А и В меняются в интервале температур 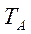 и
и 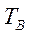 , то для расчета по (3.6) берут среднее α.
, то для расчета по (3.6) берут среднее α.
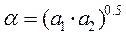
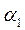 - соответствует ТА,
- соответствует ТА, 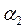 - ТВ .
- ТВ .
Окончательно уравнение линии равновесия получим в виде:
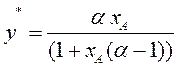 (3.7)
(3.7)
Таким образом, зная α, т.е. давление насыщенных паров чистых компонентов А и В, можно рассчитать и построить линию равновесия идеальных смесей. Это уравнение можно использовать и для нормальных растворов.
Поскольку 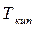 с понижением давления снижается, то α увеличивается. Относительная летучесть α при понижении температуры растет (рис.3.2). Следует отметить, что кривая равновесия и диагональ на рис. 3.2 ограничивают область существования двух фаз – пара и жидкости. Для диагонали α=1.
с понижением давления снижается, то α увеличивается. Относительная летучесть α при понижении температуры растет (рис.3.2). Следует отметить, что кривая равновесия и диагональ на рис. 3.2 ограничивают область существования двух фаз – пара и жидкости. Для диагонали α=1.
Взаимное расположение кривых на фазовых диаграммах T – x,y и y – x как для идеальных, так и для реальных систем определяются с помощью законов Коновалова. Законы Коновалова устанавливают связь между изменением состава, давления или T в 2-х фазных системах, они лежат в основе теории перегонки и ректификации бинарных смесей.
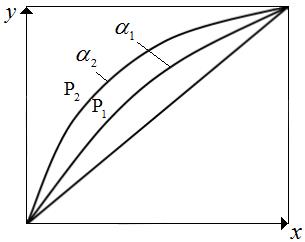
Рис.3.2 Диаграмма равновесия для бинарных смесей: 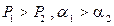 .
.
Первый закон Коновалова: пар обогащается тем компонентом, при добавлении которого к жидкости повышается давление пара над ней или снижается ее температура кипения, или пар всегда более обогащен НК, чем соответствующая ему жидкая равновесная фаза.
Этот закон дополняется первым законом Вревского, отражающим влияние T на равновесные составы фаз:
при повышении T бинарной смеси в парах возрастает относительное содержание того компонента, парциальная молярная теплота испарения которого больше. Это можно проиллюстрировать по рис. 3.1: при 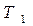 = const содержание НК в парах
= const содержание НК в парах 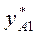 (точка
(точка 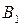 ) ,больше его содержания
) ,больше его содержания 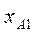 в равновесной с парами жидкости (точка
в равновесной с парами жидкости (точка 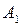 ). При добавлении к смеси НК ее температура кипения снижается, но содержание НК в паре остается выше, чем в жидкости.
). При добавлении к смеси НК ее температура кипения снижается, но содержание НК в паре остается выше, чем в жидкости.
Неидеальные растворы (реальные смеси) с полностью взаимной растворимостью компонентов не следует закону Рауля:
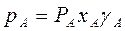 и
и 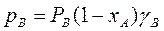 (3.8)
(3.8)
Здесь γ – коэффициент активности. Если γ>1 – положительное отклонение, если γ<1 – отрицательное. Определение γ часто затруднено, поэтому диаграмму y – x обычно строят по экспериментальным данным.
Для многих реальных смесей отклонение от закона Рауля настолько существенно, что приводит к качественно новому состоянию системы (рис.3.3).
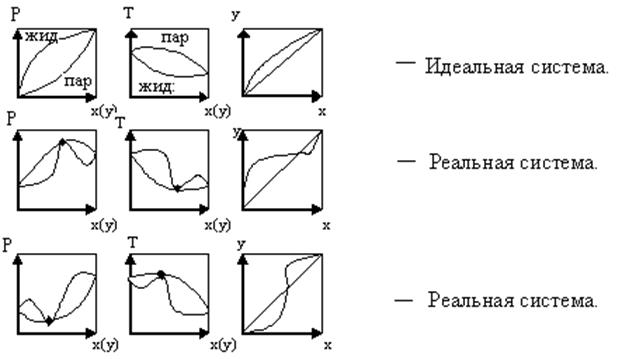
Рис.3.3 Фазовые диаграммы равновесия жидкость - пар.
В реальных системах на фазовых диаграммах P – x(y) и T – x(y) возникают относительные максимумы или минимумы. При этом кривые жидкости и пара соприкасаются друг с другом в экстремальных точках. В этих точках составы равновесных фаз одинаковы. Такие смеси называют азеотропными, или азеотропами. Такая смесь при испарении не изменяет своего состава. Поэтому для их разделения применяются специальные методы.
Для таких систем имеется второй закон Коновалова: если давление и T сосуществования 2-х бинарных фаз имеют экстремум (max или min), то составы фаз одинаковы.
При изменении внешних условий – температуры или давления значение α изменяется различно по разные стороны от точки азеотропа: одна часть «рыбка»
(б, в) должна становиться шире, другая уже.
Смещение состава азеотропов при изменении внешних условий определяется вторым законом Вревского: если давление (или T) системы жидкость – пар имеет максимум, то при повышении T в азеотропной смеси возрастает концентрация того компонента, парциальная молярная теплота испарения которого больше, а если давление (или T) система жидкость – пар имеет минимум, то при повышении T в азеотропной смеси возрастает концентрация компонента с меньшей теплотой испарения.
Этот закон определяет возможности разделения азеотропных смесей изменением давления при перегонке. При этом точка азеотропы перемещается на диаграмме y-x и в принципе может совпасть, например, с правым верхним углом диаграммы. Тогда азеотропную смесь можно разделить перегонкой.
Таким образом, законы Коновалова характеризуют изменение состояния равновесия 2-х фазных систем при изобарных или изотермических условиях, а законы Вревского определяют закономерности влияния на фазовое равновесие бинарных систем изменений температуры и давления.
Дата добавления: 2016-05-25; просмотров: 1443;
