В турбулентном течении жидкости в круглой трубе
Потери 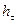 напора на трение при течении жидкости в трубах определяются формулой (6.18) Дарси-Вейсбаха
напора на трение при течении жидкости в трубах определяются формулой (6.18) Дарси-Вейсбаха
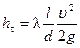 , (8.1)
, (8.1)
в которой безразмерный параметр 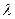 называется коэффициентом гидравлического сопротивления (для течений вязкой несжимаемой жидкости в круглой трубе
называется коэффициентом гидравлического сопротивления (для течений вязкой несжимаемой жидкости в круглой трубе 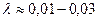 ).
).
Для ламинарного течения, которое поддается аналитическому расчету, коэффициент гидравлического сопротивления определяется формулой (7.28) Стокса 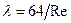 (см. п.4 гл.7), а потери напора оказываются пропорциональными первой степени средней по сечению скорости
(см. п.4 гл.7), а потери напора оказываются пропорциональными первой степени средней по сечению скорости 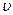 :
:
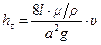 .
.
Для турбулентного течения характер сопротивления резко изменяется, линейная зависимость 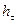 от
от 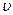 нарушается. В турбулентном режиме коэффициент гидравлического сопротивления
нарушается. В турбулентном режиме коэффициент гидравлического сопротивления 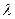 зависит уже не только от числа
зависит уже не только от числа 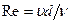 , но и от относительной эквивалентной шероховатости
, но и от относительной эквивалентной шероховатости 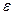 внутренней поверхности трубы, т. е.
внутренней поверхности трубы, т. е.
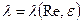 , (8.2)
, (8.2)
где 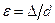 , где
, где 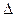 — средняя высота выступов шероховатости, причем зависимость эта имеет сложный характер.
— средняя высота выступов шероховатости, причем зависимость эта имеет сложный характер.
Предложено большое число формул для определения коэффициента 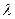 в турбулентном режиме течения; это объясняется тем, что многие из предлагаемых формул получены опытным путем. Известный российский гидромеханик И.И.Никурадзе выполнил обстоятельные исследования сопротивлений гладких и шероховатых труб. Гладкость внутренней поверхности достигалась шлифовкой труб, а шероховатость — наклеиванием на гладкую поверхность калиброванных песчинок, образующих зернистую шероховатость с разным размером зерен. Естественная шероховатость поверхностей имеет, конечно, иную форму, чем наклеенные зерна песка, поэтому в гидравлике используют понятие об абсолютной эквивалентной шероховатости
в турбулентном режиме течения; это объясняется тем, что многие из предлагаемых формул получены опытным путем. Известный российский гидромеханик И.И.Никурадзе выполнил обстоятельные исследования сопротивлений гладких и шероховатых труб. Гладкость внутренней поверхности достигалась шлифовкой труб, а шероховатость — наклеиванием на гладкую поверхность калиброванных песчинок, образующих зернистую шероховатость с разным размером зерен. Естественная шероховатость поверхностей имеет, конечно, иную форму, чем наклеенные зерна песка, поэтому в гидравлике используют понятие об абсолютной эквивалентной шероховатости  . Под этим термином понимают не среднюю высоту выступов шероховатости, а такую фиктивную зернистую равномерную шероховатость, при которой потери напора будут равными потерям напора в реальном трубопроводе при одинаковых расходах.
. Под этим термином понимают не среднюю высоту выступов шероховатости, а такую фиктивную зернистую равномерную шероховатость, при которой потери напора будут равными потерям напора в реальном трубопроводе при одинаковых расходах.
На рис. 8.3 представлены графики зависимости 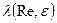 от числа Рейнольдса и относительной шероховатости
от числа Рейнольдса и относительной шероховатости 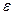 , полученные Никурадзе. Эксперименты показали, что при турбулентном режиме движения условно можно выделить три области чисел
, полученные Никурадзе. Эксперименты показали, что при турбулентном режиме движения условно можно выделить три области чисел 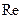 , в которых законы сопротивления различны.
, в которых законы сопротивления различны.
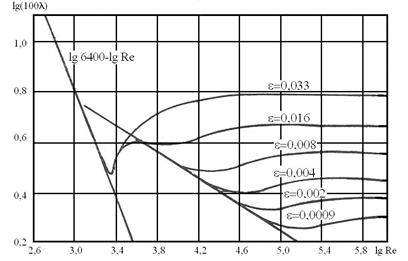
Рис. 8.3. Графики И.И. Никурадзе - зависимости 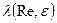
Первая область называется областью гидравлически гладких труб ( 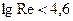 ). В этой области коэффициент
). В этой области коэффициент 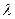 зависит только от числа Re и не зависит от шероховатости
зависит только от числа Re и не зависит от шероховатости 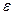 внутренней поверхности трубы. В этом случае нет различия между гладкими и шероховатыми трубами, именно поэтому физически шероховатые трубы называются гидравлически гладкими.
внутренней поверхности трубы. В этом случае нет различия между гладкими и шероховатыми трубами, именно поэтому физически шероховатые трубы называются гидравлически гладкими.
Если 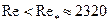 (
( 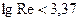 , см. гл.3), то течение жидкости – ламинарное;
, см. гл.3), то течение жидкости – ламинарное; 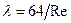 , следовательно, этот режим течения относится к течениям в области гидравлически гладких труб (зависимость
, следовательно, этот режим течения относится к течениям в области гидравлически гладких труб (зависимость 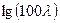 от
от 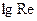 линейная).
линейная).
Если 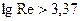 , то ламинарное течение сменяется турбулентным, причем в диапазоне чисел Рейнольдса от 2320 до
, то ламинарное течение сменяется турбулентным, причем в диапазоне чисел Рейнольдса от 2320 до 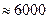 (
( 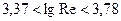 ) существует не полностью сформировавшееся турбулентное течение, а в диапазоне
) существует не полностью сформировавшееся турбулентное течение, а в диапазоне 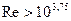 - развитое турбулентное течение.
- развитое турбулентное течение.
Для расчета коэффициента 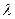 гидравлического сопротивления в диапазоне чисел Рейнольдса
гидравлического сопротивления в диапазоне чисел Рейнольдса 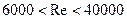 (
( 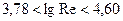 ) или даже в более широком диапазоне используются формулу Блазиуса
) или даже в более широком диапазоне используются формулу Блазиуса
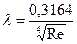 . (8.3)
. (8.3)
Трубы из цветных металлов, пластмассовые и стеклянные трубы могут считаться гидравлически гладкими практически во всем диапазоне чисел Re, а технические трубы - до значений 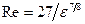 , как это принято у большинства экспериментаторов. В данном диапазоне чисел Рейнольдса потеря
, как это принято у большинства экспериментаторов. В данном диапазоне чисел Рейнольдса потеря 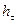 напора пропорциональна средней скорости течения в степени 1,75:
напора пропорциональна средней скорости течения в степени 1,75:
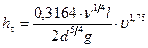 .
.
В переходной области, где турбулентное течение сформировалось не полностью 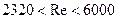 (
( 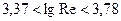 ) для расчета
) для расчета 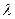 можно использовать формулу Л.А.Вулиса-И.П.Гинзбурга:
можно использовать формулу Л.А.Вулиса-И.П.Гинзбурга:
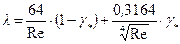 , (8.4)
, (8.4)
в которой коэффициент 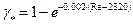 называют коэффициентом перемежаемости
называют коэффициентом перемежаемости 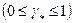 . Устройство последней формулы обеспечивает непрерывный переход от формулы Стокса (8.2) для ламинарного течения
. Устройство последней формулы обеспечивает непрерывный переход от формулы Стокса (8.2) для ламинарного течения 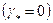 к формуле Блазиуса (8.3) для турбулентного режима течения
к формуле Блазиуса (8.3) для турбулентного режима течения 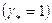 в зоне гидравлически гладких труб.
в зоне гидравлически гладких труб.
Вторая область сопротивления труб называется областью шероховатых труб: 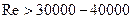 (
( 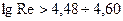 ) или, более точно:
) или, более точно: 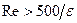 . В этой области начинает проявляться шероховатость внутренней поверхности труб и при обних и тех же числах Рейнольдса, коэффициент
. В этой области начинает проявляться шероховатость внутренней поверхности труб и при обних и тех же числах Рейнольдса, коэффициент 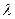 имеет различные значения для труб с разной шероховатостью. В этой области
имеет различные значения для труб с разной шероховатостью. В этой области 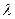
 зависит как от числа Re, так и от
зависит как от числа Re, так и от 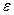 , т.е.
, т.е. 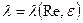 . Наиболее удобной формулой для вычисления
. Наиболее удобной формулой для вычисления 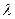 является формула А.Д. Альтшуля
является формула А.Д. Альтшуля
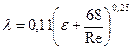 , (8.5)
, (8.5)
которая при малых значениях 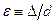 переходит в формулу Блазиуса (8.3), а при очень больших
переходит в формулу Блазиуса (8.3), а при очень больших 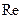 - в формулу Б.Л. Шифринсона (см.ниже). Также можно пользоваться формулой Н.З.Френкеля
- в формулу Б.Л. Шифринсона (см.ниже). Также можно пользоваться формулой Н.З.Френкеля
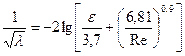 , (8.6)
, (8.6)
Третья область сопротивления труб называют областью квадратичного трения. В этой области перестают сказываться числа Рейнольдса и все определяется лишь состоянием внутренней поверхности трубы, т.е. ее шероховатостью. В области квадратичного трения 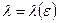 и вычисляется по формуле И.И.Никурадзе
и вычисляется по формуле И.И.Никурадзе
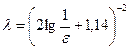 (8.7)
(8.7)
или по формуле Б.Л. Шифринсона
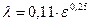 . (8.8).
. (8.8).
Третья область называется областью квадратичного трения, потому что потеря 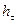 напора в случае если
напора в случае если 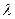 не зависит от числа
не зависит от числа 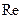 , пропорциональна квадрату средней скорости
, пропорциональна квадрату средней скорости 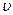 течения:
течения:
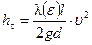 .
.
Пример. Нефть ( 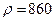
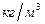 ,
, 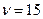 сСт) перекачивают в практически горизонтальном нефтепровод (
сСт) перекачивают в практически горизонтальном нефтепровод ( 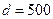 мм,
мм, 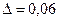 мм, l = 100 км) с расходом
мм, l = 100 км) с расходом 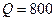 м3/ч. Определить перепад
м3/ч. Определить перепад 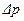 давления, необходимый для перекачки.
давления, необходимый для перекачки.
Решение. Рассчитываем скорость 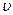 течения нефти:
течения нефти:
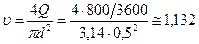
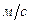 .
.
Вычисляем число Рейнольдса и относительную шероховатость:
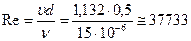 ;
; 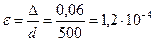 .
.
Поскольку 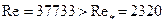 , то режим течения нефти - турбулентный. Определяем область сопротивления, для чего вычисляем граничное число Рейнольдса:
, то режим течения нефти - турбулентный. Определяем область сопротивления, для чего вычисляем граничное число Рейнольдса:
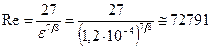 ,
,
следовательно, нужно использовать формулу Блазиуса.
Вычисляем коэффициент 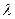 по формуле (8.3) Блазиуса:
по формуле (8.3) Блазиуса:

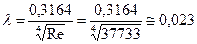 .
.
Для определения перепада 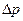 давления используем уравнение Бернулли:
давления используем уравнение Бернулли:
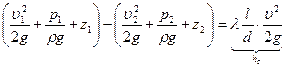 .
.
Учитывая, что 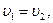
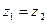 , получаем:
, получаем:
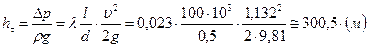 ,
,
следовательно, 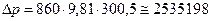 (Па).
(Па).
Ответ: 2535198 Па или 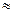 2,54 МПа (25,84 ат.).
2,54 МПа (25,84 ат.).
Дата добавления: 2016-05-16; просмотров: 2216;
