Уравнения Рейнольдса

При изучении турбулентных течений обычно вводят осредненные значения компонент скорости 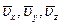давления 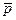, плотности 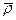, температуры 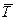(черточки над, буквами обозначают осреднение). Тогда скорость потока в каждой точке пространства в любой момент времени можно представить в виде суммы её осреднённого значения и отклонения от него:

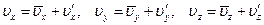, (8.9)

где 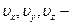действительные мгновенные скорости потока в данной точке, 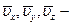осредненные по времени компоненты скоростей, 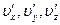— отклонения действительных скоростей от осредненных (пульсации скоростей).

Если осреднение параметров потока происходит по времени, то для любого осциллирующего параметра 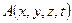его осредненное значение 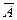находится по формуле

,

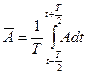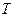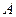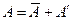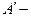где промежуток времени, называемый периодом осреднения, достаточно велик по отношению ко времени отдельных пульсаций и мал по отношению ко времени заметного изменения средних характеристик. Если представить параметр в виде суммы , где пульсационная составляющая, то .

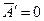Воспользуемся уравнениями движения сплошной среды в напряжениях, выражающими 2-й закон Ньютона (см. гл.1). Для несжимаемой жидкости при отсутствии массовых сил эти уравнения имеют вид:

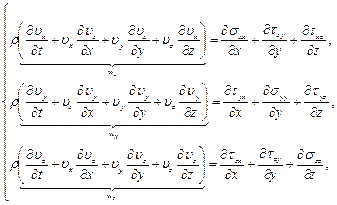(8.10)

Учитывая уравнение неразрывности

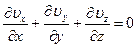, (8.11)

эту систему уравнений можно записать в равносильной форме:

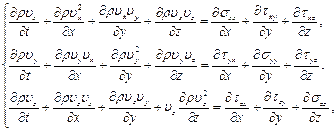(8.12)

Если часть членов в системе (8.12) перенести из левой части уравнений в правую, то систему можно представить в другом виде:

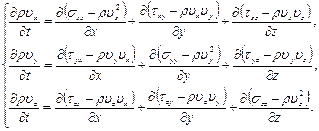(8.13)

Согласно (8.9) представим каждый параметр, входящий в систему уравнений (8.13), в виде его осредненного значения и осциллирующей составляющей. Выполним осреднение уравнений (8.13) с учетом следующих свойства операции осреднения:

среднее значение пульсации равно нулю, ;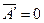

среднее значение суммы параметров равно сумме средних значений этих параметров, ;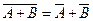

среднее значение производной от истинной характеристики турбулентного движения равняется производной от ее среднего значения ;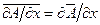

среднее значение произведения двух сомножителей, из которых только один испытывает турбулентные пульсации, равно нулю, ;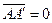

осредненное значение произведения двух пульсирующих величин равняется сумме произведения средних величин и среднего значения произведения пульсаций этих величин, .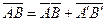

Как результат осреднения получим систему уравнений:

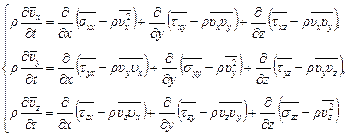(8.14)

Заметим далее, что 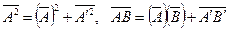, получим

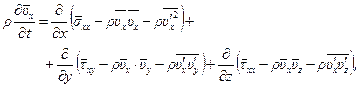
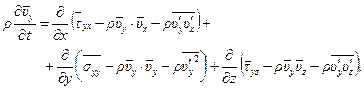
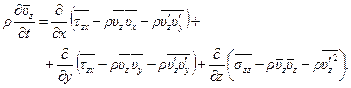
Наконец, полученную систему уравнений можно переписать в равносильном виде, если принять во внимание осредненное уравнение неразрывности

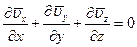. (8.15)

Выполнив соответствующие преобразования, придем к системе уравнений, называемых уравнениями Рейнольдса

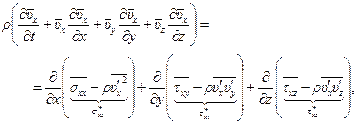
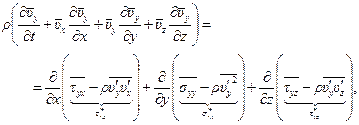(8.16)

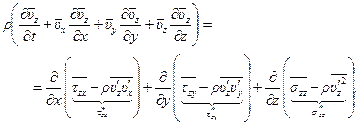
Эти уравнения отличаются от уравнений движения в напряжениях (8.4) лишь тем, что к осредненным напряжениям добавились дополнительные слагаемые, представляющие собой осредненные значения произведений осциллирующих составляющих скорости течения. Эти слагаемые называют рейнольдсовскими напряжениями в честь крупнейшего английского инженера и ученого Осборна Рейнольдса (1842-1912), много сделавшего для развития теории турбулентности.

Таким образом, показано, что для осредненных параметров турбулентного течения справедливы такие же уравнения (8.10), что и для ламинарного течения, однако тензор напряжений в турбулизованной среде имеет более сложный вид:

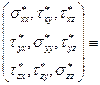
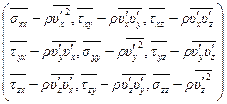. (8.17)