Распределение скорости жидкости в сечении трубы

Зная распределение касательного наряжения по радиусу трубы, из уравнения (7.1) можно найти распределение скорости 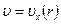течения жидкости. Для этого разрешим уравнение (7.1) относительно :

,

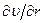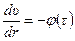где 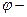функция, обратная функции 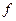. Кроме того, здесь учтено, что 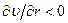. Используя далее (7.9), получаем дифференциальное уравнение для распределения скорости :

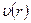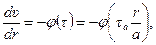. (7.10)

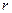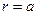Интегрируя это уравнение по от до 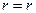, и принимая во внимание условие 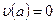(условие прилипания), получаем:

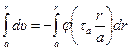
или

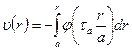. (7.11)

Сделаем замену переменной согласно равенствам

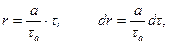(7.12)

учитывая, что 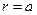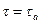при , ; при 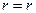; 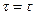. Тогда из (7.11) получим:

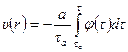(7.13)

Формула (7.13) позволяет находить закон распределения скорости 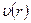жидкости по радиусу трубы при любом виде функции .

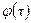Расход жидкости

Для вычисления объемного расхода 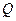жидкости в круглой трубе учтем, что элементарный расход 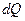жидкости через кольцевое сечение, заключенное между концентрическими окружностями с радиусам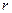и и 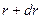, выражается равенством

,

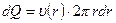следовательно, полный расход представляется интегралом:

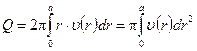. (7.14)

Выполняя интегрирование «по частям», находим:

.

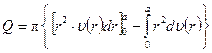Учитывая, что 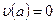и 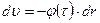, получаем:

,

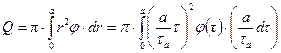и, наконец, имеем формулу для вычисления расходаа жидкости:

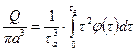. (7.15)