Распределение касательного напряжения
В сечении трубы
Выделим в жидкости, движущейся в трубе, цилиндр радиуса 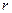 с длиной
с длиной 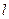 (рис. 7.1.).
(рис. 7.1.).
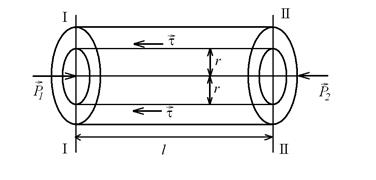
Рис. 7.1. Равновесие сил на поверхности цилиндра
Рассмотрим силы, действующие на выделенный цилиндр. В сечении (1—1) действует сила давления 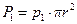 , в сечении (2—2) - сила
, в сечении (2—2) - сила 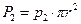 , где
, где 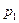 и
и 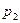 давления в сечениях (1—1) и (2—2). На боковую поверхность цилиндра действует сила трения
давления в сечениях (1—1) и (2—2). На боковую поверхность цилиндра действует сила трения 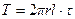 . Кроме того, имеется еще массовая сила – сила инерции равняя массе
. Кроме того, имеется еще массовая сила – сила инерции равняя массе 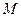 жидкости выделенного объема, умноженной на ускорение
жидкости выделенного объема, умноженной на ускорение 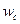 его центра тяжести со знаком «минус».
его центра тяжести со знаком «минус».
Уравнение равновесия всех этих сил в проекции на ось трубы имеет вид:
 . (7.6)
. (7.6)
Поскольку движение жидкости считается установившимся, то 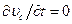 . Кроме того, из уравнения неразрывности следует, что
. Кроме того, из уравнения неразрывности следует, что 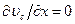 , следовательно, ускорение
, следовательно, ускорение 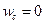 . Действительно
. Действительно
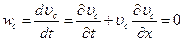 .
.
Тогда из уравнения (7.6) баланса сил заключаем, что распределение модуля 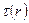 касательного напряжения по радиусу трубы будет линейным:
касательного напряжения по радиусу трубы будет линейным:
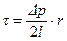 , (7.7)
, (7.7)
где 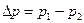 . В частности, модуль
. В частности, модуль 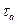 касательного напряжения на внутренней поверхности трубы
касательного напряжения на внутренней поверхности трубы 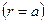 выражается формулой
выражается формулой
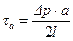 . (7.8)
. (7.8)
Используя (7.8), распределению (7.7) можно придать следующий вид:
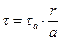 . (7.9)
. (7.9)
Отсюда видно, что касательное напряжение минимально 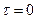 на оси трубы (
на оси трубы ( 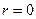 ) и максимально
) и максимально 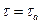 на внутренней поверхности трубы
на внутренней поверхности трубы 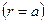 .
.
Дата добавления: 2016-05-16; просмотров: 598;
