ЛАМИНАРНОЕ ТЕЧЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
Рассмотрим установившееся ламинарное течение несжимаемой жидкости в круглой трубе, линиями тока которого будут прямые, параллельные оси и образующим стенки трубы. Направим ось ОХ по оси трубы, так что поперечное сечение трубы лежит в плоскости  . Тогда
. Тогда  и остается лишь одна отличная от нуля компонента скорости
и остается лишь одна отличная от нуля компонента скорости 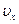 . Из уравнения неразрывности (5.4) следует, что
. Из уравнения неразрывности (5.4) следует, что
 ,
,
т. е. компонента 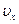 не зависит от
не зависит от  , а является функцией лишь
, а является функцией лишь 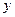 и
и 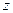 . Однако вследствие радиальной симметрии течения функция
. Однако вследствие радиальной симметрии течения функция  определяется не самими координатами
определяется не самими координатами 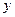 и
и 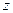 , а лишь их комбинацией
, а лишь их комбинацией  , являющейся расстоянием точки сечения трубы от ее оси:
, являющейся расстоянием точки сечения трубы от ее оси: 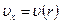 .
.
Связь касательного напряжения 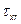 между слоями жидкости и разностью скоростей этих слоев, рассчитанной на единицу расстояния между ними
между слоями жидкости и разностью скоростей этих слоев, рассчитанной на единицу расстояния между ними  (градиентом скорости) в общем случае можно записать как
(градиентом скорости) в общем случае можно записать как
 . (7.1)
. (7.1)
Для различных жидкостей эта связь может иметь различный вид, однако, отметим два частных случая, имеющих, однако, широкое применение в практике.
1. Функция 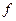 есть линейная функция своего аргумента, причем
есть линейная функция своего аргумента, причем 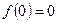 :
:
 . (7.2)
. (7.2)
Жидкость, удовлетворяющую реологическому соотношению (7.2), называют ньютоновской вязкой жидкостью, а коэффициент пропорциональности  - динамической вязкостью этой жидкости. Очевидно, что размерность
- динамической вязкостью этой жидкости. Очевидно, что размерность  , причем в системе СИ единицей измерения динамической вязкости служит величина
, причем в системе СИ единицей измерения динамической вязкости служит величина  , называемая одним Пуазом:
, называемая одним Пуазом:  .
.
Условие 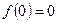 означает, что при отсутствии скорости движения слоев жидкости друг относительно друга (скорости сдвига) касательное напряжение между слоями равно нулю.
означает, что при отсутствии скорости движения слоев жидкости друг относительно друга (скорости сдвига) касательное напряжение между слоями равно нулю.
Поскольку слои жидкости, расположенные ближе к оси трубы, движутся быстрей, чем слои жидкости, расположенные дальше от нее,  , следовательно,
, следовательно, 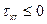 , т.е. медленные слои тормозят быстрые. Если вместо касательного напряжения
, т.е. медленные слои тормозят быстрые. Если вместо касательного напряжения 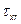 ввести его модуль
ввести его модуль  , который в рассматриваемом случае равен
, который в рассматриваемом случае равен 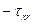 , то формула (7.2) приобретет вид:
, то формула (7.2) приобретет вид:
 (7.3)
(7.3)
2. Функция 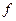 есть степенная функция своего аргумента. Говоря точней, модуль касательного напряжения является степенной функцией модуля скорости сдвига
есть степенная функция своего аргумента. Говоря точней, модуль касательного напряжения является степенной функцией модуля скорости сдвига  , причем, так же как и в предыдущем случае,
, причем, так же как и в предыдущем случае, 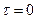 при
при 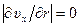 . Иными словами, имеет место соотношение
. Иными словами, имеет место соотношение
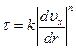 , (7.4)
, (7.4)
а само реологическое уравнение (7.1) может быть представлено в виде:
 . (7.5)
. (7.5)
Такая запись показывает, что модуль касательного напряжения дается формулой (7.4), а его знак совпадает со знаком производной  .
.
Жидкость, удовлетворяющую реологическому соотношению (7.4), называют неньютоновской степенной жидкостьюили степенной жидкостью Освальда. Коэффициент  , входящий в это уравнение, называют косистентностью жидкости, а
, входящий в это уравнение, называют косистентностью жидкости, а  показателем степени: если
показателем степени: если  , то жидкость называют псевдопластичной, если же
, то жидкость называют псевдопластичной, если же  дилатантной. Размерность
дилатантной. Размерность  консистентности равна, очевидно,
консистентности равна, очевидно,  . При
. При 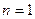 степенная жидкость является ньютоновской вязкой жидкостью, причем коэффициент
степенная жидкость является ньютоновской вязкой жидкостью, причем коэффициент  .
.
Дата добавления: 2016-05-16; просмотров: 662;
