Жидкости в круглой трубе

Распределение скорости. При ламинарном течении ньютоновской вязкой несжимаемой жидкости в трубе связь касательного напряжения и градиента скорости имеет вид:

,

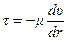т.е.

.

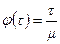На основе формулы (7.13) можно найти распределение скорости :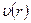

.

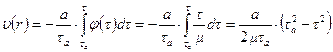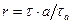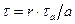Переходя к переменной или , получаем:

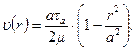
Согласно (7.8), 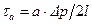, поэтому искомое распределение скорости имеет вид:

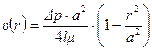. (7.16)

Таким образом, эпюрой скорости ламинарного течения ньютоновской вязкой несжимаемой жидкости является параболоид вращения с меридиональным сечением, представляющим собой параболу (рис. 7.2).

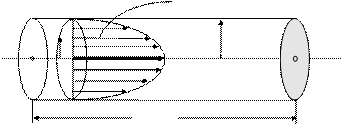
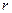
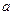
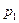
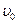
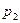
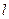
Рис. 7.2.Распределение скорости по сечению трубы

Максимальное значение 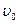скорости жидкости достигается на оси трубы (т.е. при ):

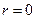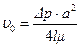, (7.17)

поэтому распределение (7.16) можно представить в виде:

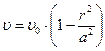. (7.18)

Расход жидкости. Расход вязкой ньютоновской жидкости вычисляем по формуле (7.15), полагая в ней 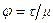. Имеем:

.

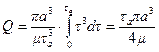Используя соотношение (7.5), находим:

.

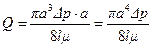Если вместо радиуса 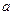трубы ввести ее внутренний диаметр 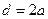, получим:

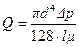. (7.19)

Соотношение (7.19) называется формулой Пуазейля по имени французского врача и физиолога, исследовавшего законы движения крови по капиллярным сосудам и получившего эту зависимость. Формула Пуазейля показывает, что при установившемся ламинарном движении вязкой ньютоновской жидкости в круглой трубе объемный расход пропорционален перепаду давления, рассчитанному на единицу длины трубы, четвертой степени ее радиуса и обратно пропорционален вязкости жидкости.

Средняя скорость течения. Расход жидкости можно записать через осевую скорость 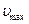, используя соотношение (7.17):

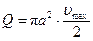. (7.20)

Поскольку средняя по сечению скорость 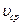жидкости в трубе выражается через расход 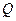посредством равенства

,

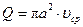то, сравнив его с (7.20), получим, что

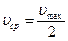. (7.21)

Таким образом, средняя по сечению скорость жидкости равна половине максимальной скорости, достигаемой на оси трубы.

Потери напора на трение при ламинарном течении.Уравнение Бернулли, записанное для горизонтальной трубы постоянного диаметра, имеет вид:

,

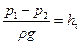где 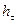— потеря напора на трение между сечениями (1—1) и (2—2). Следовательно,

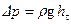. (7.22).

Подставив (7.22) в (7.18), найдем, что

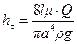, (7.23)

или

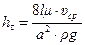. (7.24)

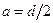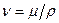Положив и , где 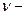коэффициент кинематической вязкости, получим:

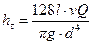. (7.25)

Из (7.25) следует, что потеря напора на трение при ламинарном режиме движения пропорциональна расходу и вязкости жидкости и обратно пропорциональна диаметру в четвертой степени.

Коэффициент гидравлического сопротивления. Потерю напора на трение можно представить в ином виде, если ввести число Рейнольдса.

.

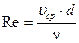Воспользовавшись формулой (7.24), получим

.

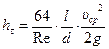Обозначив коэффициент 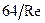через 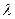, получим

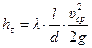. (7.27)

Это соотношение называют формулой Дарси-Вейсбаха, а входящий в нее коэффициент 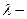коэффициентом гидравлического сопроивления.

Таким образом, для ламинарного течения вязкой несжимаемой жидкости в круглой трубе коэффициент 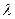выражается встретившейся ранее формулой Стокса

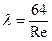. (7.28)

Коэффициент Кориолиса.При ламинарном течении вязкой жидкости в круглой трубе коэффициент Кориолиса можно рассчитать теоретическим путем. В гл.4 для этого коэффициента было получено выражение

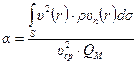, (7.28)

где .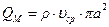

В рассматриваемом случае 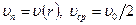, поэтому (7.28) можно представить в виде:

.

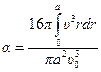Подставив в эту формулу распределение скорости из (7.18), получим:

.

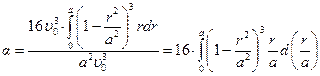Для вычисления интеграла в полученном выражении введем безразмерную переменную 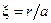, тогда

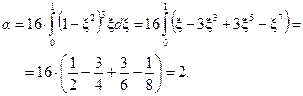
Следовательно, при ламинарном течении вязкой несжимаемой жидкости в круглой трубе коэффициент Кориолиса равен 2.

Пример 1. Каков минимальный диаметр 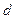круглой трубы ( 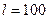см), способный обеспечить расход жидкости ( 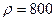кг/м³, 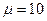сПз) не более 100 см³/с, если известно, что перепад давления между ее концами не может превышать 490 Па?

Решение. Предположим, что течение жидкости в трубе - ламинарное, тогда из формулы (7.19) Пуазейля следует:

.

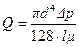
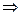
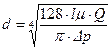Подставив сюда максимально возможный расход жидкости 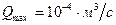(100 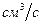), заметим, что диаметр трубы будет минимальным в том случае, если перепад давления 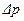, стоящий в знаменателе дроби, будет максимальным, т.е. 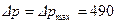Па. После этого имеем:

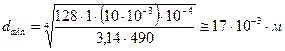(или 17 мм).

Итак, минимальный диметр трубы найден, однако решение задачи не закончено. Необходимо проверить справедливость предположения о ламинарном характере течения. Для этого сначала найдем среднюю скорость 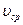жидкости:

,

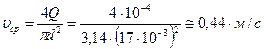а затем вычислим число Рейнольдса:

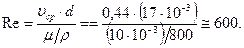
Поскольку вычисленное значение числа Рейнольдса оказалось меньше критического 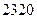, то течение действительно будет ламинарным, и сделанное предположение верно.

Ответ: d = 17 мм.

Пример 2. По горизонтальному трубопроводу с диаметром 205 мм и длиной 4 км перекачивают топочный мазут, кинематическая вязкость которой равна 1,0 Ст, а плотность - 890 кг/м³ Определить перепад давлений, необходимый для перекачки указанного нефтепродукта с расходом 25 т/ч.

Решение. Прежде всего, выясним режим перекачки. Сначала вычислим среднюю скорость течения мазута

.

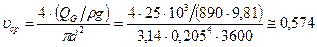
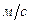Теперь можно найти число Рейнольдса:

.

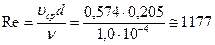Поскольку 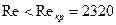, то течение жидкости в трубе будет ламинарным, поэтому коэффициент 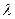гидравлического сопротивления определяется формулой (7.28):

,

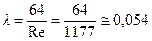а перепад 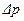давления рассчитывается по формуле (7.27) Дарси-Вейсбаха (или по формуле (7.19) Пуазейля):

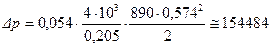Па.

Ответ: 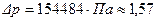атм.

Пример 3. Определить расход жидкосчти в горизонтальном нефтепроводе, имеющем диаметр 309 мм и длину 30 км, по которому перекачивают высоковязкую нефть с плотностью 870 кг/м³ и вязкостью 135 сСт, если известно, что движущий перепад давлений равен 8 amм.

Решение. Поскольку режим течения нефти неизвестен, то предположим сначала, что он ламинарный, а затем проверим сделанное допущение.

Если течение нефти ламинарное, то коэффициент 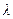гидравлического сопротивления определяется формулой (7.28) Стокса: 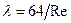. Используя формулу (7.27) закона Дарси-Вейсбах, имеем:

,

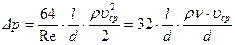откуда находим среднюю скорость течения нефти:

.

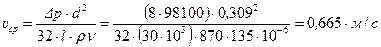Вычисляем число Рейнольдса.

.

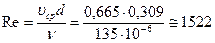Поскольку 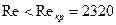, то исходное предположение о характере течения оказалось верным.

Рассчитываем объемный расход перекачки:

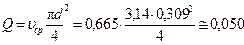м³/с ( ).

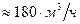Заметим, если бы число Рейнольдса оказалось большим, чем 2320, то расчет следовало бы повторить, но уже воспользовавшись другими формулами для 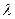, справедливыми, в частности, для турбулентного режима.

Ответ: 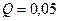м³/с.