Объемный, массовый и весовой расходы

Рассмотрим некоторую поверхность 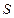, опирающуюся на контур (рис. 3.2), и вычислим объем жидкости, протекающей в единицу времени через эту поверхность.

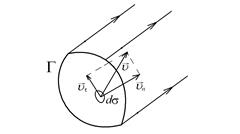
Рис. 3.2.Трубка тока в жидкости

Для этого разложим вектор скорости в каждой точке рассматриваемой поверхности на касательную и нормальную составляющие 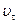, и 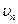. Понятно, что объем жидкости, протекающей в единицу времени через поверхность 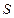, определяется только нормальной составляющей вектора скорости и дается формулой:

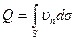
где 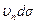— объем жидкости, протекающей в единицу времени через элемент 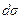поверхности .

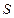Величину объема жидкости, протекающей в единицу времени через поверхность 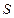, называют объемным расходом жидкости через рассматриваемую поверхность.

Соответственно величины

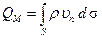
и

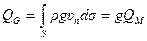
называют массовым и весовым расходами жидкости.

Единицы измерения всех расходов приведены в таблице 3.1.

Таблица 3.1

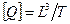
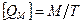
Расходы	Объемный	Массовый	Весовой
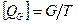
СИ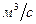

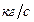
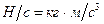
В случае если течение жидкости является установившимся, величина каждого расходов не зависит от формы поверхности 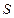, опирающейся на контур . Если взять, например, две различные поверхност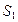и и 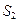, опирающиеся на один и тот же контур , то расходы 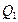и 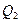через них должны быть равны друг другу. В противном случае в области между этими поверхностями объем (масса, вес) жидкости должен был бы изменяться, что противоречит условию об установившемся характере течения.

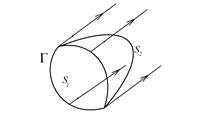
Рис. 3.3.К доказательству независимости расхода жидкости от сечения трубки тока в установившемся режиме течения

С понятием расход жидкости связана одна из важнейших в гидравлике характеристик течения жидкости в трубопроводе - средняя по сечению скорость жидкости. Если образующие поверхности трубопровода параллельны друг другу, то средняя скорость течения – это такая скорость 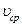, которая, будучи умноженная на площадь 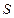поперечного сечения трубопровода, дает расход 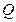жидкости. Иными словами,

.