Переход от ламинарного течения в трубе к турбулентному

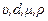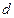Выясним условия (критерии) перехода течения от ламинарного к турбулентному режиму в трубопроводе круглого поперечного сечения. Предположим, что процесс течения жидкости определяется набором параметров , где — внутренний диаметр трубы, 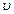— средняя скорость течения жидкости. Если величины 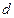, 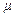и 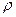неизменны, а 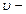скорость течения жидкости постепенно увеличивается, то при некотором критическом значении 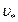скорости ламинарное течение потеряет устойчивость и станет турбулентным.

Критическое значение скорости, при которой течение становится турбулентным, определяется параметрам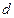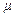и , и :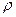

.

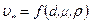Разделив обе части этого равенства на 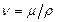( 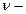коэффициент кинематической вязкости жидкости), придадим ему следующий вид:

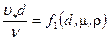(3.1)

где .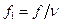

В левой части последнего равенства стоит безразмерный параметр 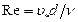, называемый критическим числом Рейнольдса. То, что этот параметр безразмерный, следует из анализа размерностей величин, из которых он образован:

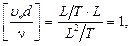
Возникает кажущееся противоречие: с одной стороны, значение левой части равенства (3.1) не зависит от выбора системы единиц, в которой производятся вычисления. С другой стороны, аргументы функции 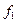, стоящей в правой части того же равенства, размерные величины, т.е. их численные значения могут быть произвольными в зависимости, от выбора системы единиц измерения. Следовательно, при произвольном изменении значений аргументов функции 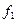, величина 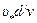самой функции остается неизменной. Это может быть только в случае, если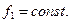

Таким образом, смена режима течения определяется безразмерным числом

,

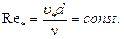которое в этот момент принимает некоторое критическое значение.