Движущейся с постоянным ускорением
Рассмотрим цистерну, частично заполненную жидкостью и движущуюся по прямой с постоянным ускорением 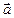 (рис. 2.20). Если систему отсчета связать с цистерной, то жидкость в такой системе будет находиться в относительном покое.
(рис. 2.20). Если систему отсчета связать с цистерной, то жидкость в такой системе будет находиться в относительном покое.
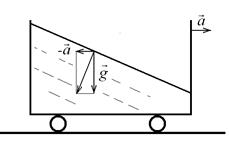
Рис. 2.20.Относительное равновесие жидкости в цистерне, движущейся с постоянным ускорением
В рассматриваемом случае компоненты вектора 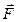 массовых сил и составляющие вектора
массовых сил и составляющие вектора 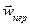 переносного ускорения имеют вид:
переносного ускорения имеют вид:
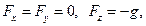
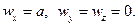
Уравнения Эйлера (2.36), записанные в форме полного дифференциала, дают в рассматриваемом случае следующее выражение:
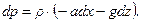 (2.44)
(2.44)
Интегрируя это уравнение, получаем:
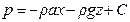 , (2.45)
, (2.45)
где 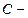 постоянная интегрирования. Для того чтобы найти эту постоянную, предположим, что
постоянная интегрирования. Для того чтобы найти эту постоянную, предположим, что 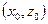 - какая-нибудь точка свободной поверхности жидкости в цистерне. Поскольку давление в этой точке известно и равно
- какая-нибудь точка свободной поверхности жидкости в цистерне. Поскольку давление в этой точке известно и равно 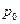 , то имеем:
, то имеем:
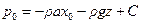
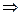
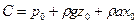 .
.
Подставляя 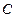 в (2.45), получаем формулу для распределения давления в цистерне:
в (2.45), получаем формулу для распределения давления в цистерне:
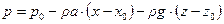 . (2.46)
. (2.46)
Поверхностями равного давления 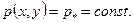 , в т.ч., и свободная поверхность жидкости, являются плоскости, уравнения которых имеют вид:
, в т.ч., и свободная поверхность жидкости, являются плоскости, уравнения которых имеют вид:
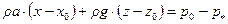 ,
,
причем свободная поверхность жидкости 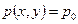 имеет уравнение
имеет уравнение
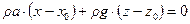 . (2.47)
. (2.47)
Отсюда видно, что свободная поверхность жидкости перпендикулярна вектору с координатами 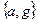 . Угол наклона этой плоскости к горизонту, определяется равенством
. Угол наклона этой плоскости к горизонту, определяется равенством 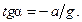
Пример 1. В открытом цилиндрическом сосуде радиуса 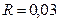 м находится вода, уровень которой составляет
м находится вода, уровень которой составляет 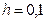 м. С какой угловой скоростью
м. С какой угловой скоростью 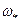 должен вращаться этот сосуд вокруг своей вертикальной оси, чтобы свободная поверхность жидкости касалась дна?
должен вращаться этот сосуд вокруг своей вертикальной оси, чтобы свободная поверхность жидкости касалась дна?
Решение. Используя формулу (2.42), имеем:
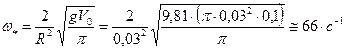 .
.
Ответ: 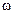 = 66 с-1.
= 66 с-1.
Пример 2. Открытый цилиндрический сосуд радиуса 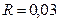 м содержит
м содержит 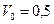 л воды. В боковой поверхности сосуда на высоте
л воды. В боковой поверхности сосуда на высоте 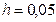 м от дна имеется малое отверстие, закрытое пробкой. Найти максимальную угловую скорость, с которой может вращаться сосуд вокруг своей вертикальной оси, чтобы пробка, рассчитанная на перепад давлений не более
м от дна имеется малое отверстие, закрытое пробкой. Найти максимальную угловую скорость, с которой может вращаться сосуд вокруг своей вертикальной оси, чтобы пробка, рассчитанная на перепад давлений не более 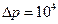 Па, не вылетела из отверстия.
Па, не вылетела из отверстия.
Решение. Используя формулу (2.39), имеем:
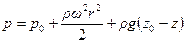 .
.
Отсюда находим давление на стенке сосуда 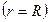 на высоте
на высоте 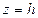 от его дна:
от его дна:
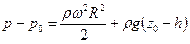 .
.
Выразив 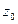 , согласно (2.41), через объем
, согласно (2.41), через объем 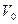 жидкости в сосуде
жидкости в сосуде
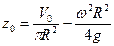 ,
,
и подставив найденное значение в предыдущее уравнение, получим:
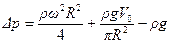 ,
,
где 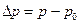 . Отсюда видно, что по мере увеличения угловой скорости вращения цилиндра увеличивается перепад давлений в рассматриваемой точке его стенки. Максимальная угловая скорость
. Отсюда видно, что по мере увеличения угловой скорости вращения цилиндра увеличивается перепад давлений в рассматриваемой точке его стенки. Максимальная угловая скорость 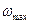 вращения цилиндра, при которой будет достигрут перепад
вращения цилиндра, при которой будет достигрут перепад 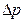 давления, определится выражением
давления, определится выражением
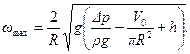
Подставив сюда численные данные, найдем:
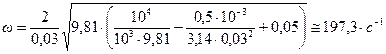 .
.
Ответ: 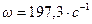 .
.
Пример 3. Определить угол 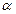 наклона свободной поверхности нефти к горизонту при торможении железнодорожной цистерны, происходящим с постоянным ускорением
наклона свободной поверхности нефти к горизонту при торможении железнодорожной цистерны, происходящим с постоянным ускорением 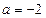 м/с2.
м/с2.
Решение. Тангенс угла 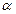 наклона к горизонту поверхности жидкости в цистерне определяется формулой
наклона к горизонту поверхности жидкости в цистерне определяется формулой
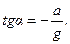
Отсюда находим:
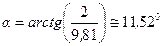 .
.
Ответ: 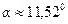 .
.
Дата добавления: 2016-05-16; просмотров: 2878;
