ЛИНЕЙНЫЕ ОДНОРОДНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим ЛОСУ п-го порядка с постоянными коэффициентами
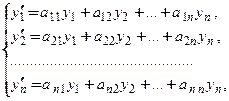 (12)
(12)
в которой искомыми являются функции 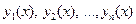 действительной переменной х,
действительной переменной х,
коэффициенты 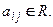 Эту систему можно записать в матричной форме (см. раздел 8.3.2):
Эту систему можно записать в матричной форме (см. раздел 8.3.2):
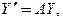 (13)
(13)
где 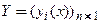 − искомое решение,
− искомое решение, 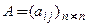 − числовая матрица.
− числовая матрица.
Система (13) всегда обладает тривиальным решением 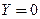 , в чем легко убедиться непосредственной подстановкой:
, в чем легко убедиться непосредственной подстановкой: 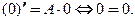 Запишем решение в виде
Запишем решение в виде
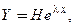 (14)
(14)
где  − числовая матрица-столбец,
− числовая матрица-столбец, 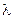 − неизвестное число. Такое представление решения называют подстановкой Эйлера. При помощи этой подстановки поиск неизвестных функций сводится к алгебраической задаче поиска наборов чисел
− неизвестное число. Такое представление решения называют подстановкой Эйлера. При помощи этой подстановки поиск неизвестных функций сводится к алгебраической задаче поиска наборов чисел 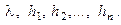
Подставим решение (14) в систему (13): 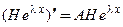 . Найдем производную:
. Найдем производную: 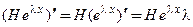 и исключим ее из матричного уравнения:
и исключим ее из матричного уравнения: 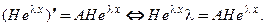 Соберем все члены уравнения в левой части:
Соберем все члены уравнения в левой части: 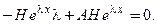 Вынесем общие множители, сократим на
Вынесем общие множители, сократим на  и получим уравнение:
и получим уравнение:
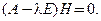 (15)
(15)
Этому матричному уравнению соответствует система линейных однородных алгебраических уравнений, в скалярной форме имеющая вид:
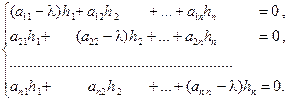 (16)
(16)
Нужно найти все значения 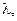 при которых существуют нетривиальные решения
при которых существуют нетривиальные решения 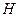 системы (16). Такую задачу называют задачей о собственных числах и векторах матрицы А. Из курса линейной алгебры [4, 6] известно, что необходимым и достаточным условием существования нетривиального решения однородной системы (16) является равенство определителя системы нулю:
системы (16). Такую задачу называют задачей о собственных числах и векторах матрицы А. Из курса линейной алгебры [4, 6] известно, что необходимым и достаточным условием существования нетривиального решения однородной системы (16) является равенство определителя системы нулю:
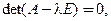 или
или 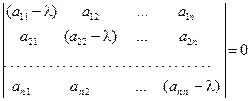 . (17)
. (17)
Выражением для определителя (17) является многочлен п-й степени 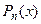 с действительными коэффициентами. Уравнение (17) и многочлен
с действительными коэффициентами. Уравнение (17) и многочлен 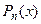 называют характеристическими. Далее нужно решить характеристическое уравнение (найти собственные числа), и изсистемы (16) для каждого собственного числа в зависимости от его кратности найти один или несколько соответствующих собственных векторов
называют характеристическими. Далее нужно решить характеристическое уравнение (найти собственные числа), и изсистемы (16) для каждого собственного числа в зависимости от его кратности найти один или несколько соответствующих собственных векторов 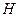 матрицы А.
матрицы А.
У многочлена п-й степени 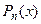 с действительными коэффициентами корнями могут быть как действительные, так и комплексные числа (см. раздел 1.1.6). Рассмотрим четыре случая.
с действительными коэффициентами корнями могут быть как действительные, так и комплексные числа (см. раздел 1.1.6). Рассмотрим четыре случая.
1. Пусть все корни характеристического уравнения − различные действительные числа 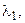
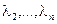 кратности 1, которым соответствуют собственные векторы
кратности 1, которым соответствуют собственные векторы 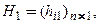
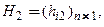 …,
…, 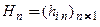 . Тогда соответствующие решения имеют вид
. Тогда соответствующие решения имеют вид
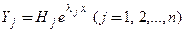 (18)
(18)
и образуют фундаментальную систему решений. В этом случае общее решение системы 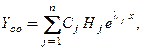 где
где 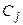 − произвольные постоянные.
− произвольные постоянные.
2. Пусть 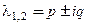 − пара комплексно-сопряженных корней уравнения (17) кратности 1. Если собственному числу
− пара комплексно-сопряженных корней уравнения (17) кратности 1. Если собственному числу 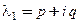 соответствует собственный вектор
соответствует собственный вектор 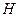 , то решение
, то решение 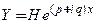 имеет комплексные элементы. Можно доказать, что действительная и мнимая части этого решения
имеет комплексные элементы. Можно доказать, что действительная и мнимая части этого решения
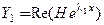 и
и 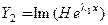 (19)
(19)
также являются решениями системы, линейно независимыми между собой.
Заметим, что из пары комплексно-сопряженных корней достаточно взять только один, так как действительные решения, соответствующие второму корню  , совпадают с точностью до знака с полученными выше для корня
, совпадают с точностью до знака с полученными выше для корня 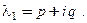
3. Пусть 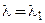 − действительный корень уравнения (17) кратности
− действительный корень уравнения (17) кратности 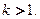
Если число линейно независимых собственных векторов 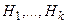 равно кратности
равно кратности 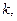 то набор из
то набор из 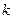 соответствующих частных решений ЛОСУ, линейно независимых между собой, записывается так:
соответствующих частных решений ЛОСУ, линейно независимых между собой, записывается так:
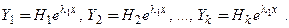 (20)
(20)
Если число  соответствующих линейно независимых собственных векторов меньше кратности
соответствующих линейно независимых собственных векторов меньше кратности 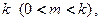 то частное решение системы представимо в виде:
то частное решение системы представимо в виде:
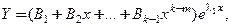 (21)
(21)
где 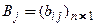 − неизвестные векторы. Чтобы найти компоненты векторов
− неизвестные векторы. Чтобы найти компоненты векторов 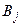 , нужно подставить (21) в систему (13) и найти их из условия тождественного равенства левой части ЛОСУ нулю. В результате подстановки получим систему линейных однородных алгебраических уравнений, содержащей ровно
, нужно подставить (21) в систему (13) и найти их из условия тождественного равенства левой части ЛОСУ нулю. В результате подстановки получим систему линейных однородных алгебраических уравнений, содержащей ровно 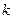 свободных переменных, которые следует обозначить буквами
свободных переменных, которые следует обозначить буквами 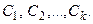 Тогда формула (21) описывает компоненту общего решения однородной системы. Здесь было приведено краткое описание метода неопределенных коэффициентов.
Тогда формула (21) описывает компоненту общего решения однородной системы. Здесь было приведено краткое описание метода неопределенных коэффициентов.
4. Пусть 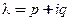 − комплексный корень уравнения (17) кратности k, которому соответствует k собственныx комплексных векторов. Тогда набор из
− комплексный корень уравнения (17) кратности k, которому соответствует k собственныx комплексных векторов. Тогда набор из 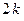 соответствующих частных решений, линейно независимых между собой, имеет вид:
соответствующих частных решений, линейно независимых между собой, имеет вид:
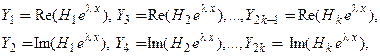 (22)
(22)
где 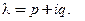 Как и во втором случае, сопряженное комплексное число
Как и во втором случае, сопряженное комплексное число  также является корнем кратности k, и набор частных решений, соответствующих этому корню, совпадает с набором (22) для корня
также является корнем кратности k, и набор частных решений, соответствующих этому корню, совпадает с набором (22) для корня 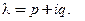
Если число собственных векторов меньше кратности 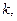 то целесообразно решать систему другими методами: сведением к дифференциальному уравнению или методом неопределенных коэффициентов.
то целесообразно решать систему другими методами: сведением к дифференциальному уравнению или методом неопределенных коэффициентов.
Можно доказать, что решения, соответствующие разным корням характеристического уравнения, линейно независимы между собой. Изложенная выше процедура позволяет построить фундаментальную систему в виде объединение всех частных линейно независимых решений и найти общее решение.
Алгоритм 4 решения однородной системы с постоянными коэффициентами
1. Составить систему (16) и характеристическое уравнение (17).
2. Найти все корни уравнения (17) и определить их кратности.
3. Для каждого найденного корня найти набор собственных векторов из системы (16) и написать соответствующие частные решения по формулам, подходящим конкретному случаю из числа формул (18) − (22).
Если число линейно независимых собственных векторов меньше кратности корня, то описываемый алгоритм не применим и нужно использовать метод неопределенных коэффициентов или переход к дифференциальному уравнению.
4. Составить фундаментальную систему решений и записать общее решение по
формуле (11).
Дата добавления: 2016-05-25; просмотров: 1150;
