Статистическая гипотеза. Статистический критерий
Под статистической гипотезой (или просто гипотезой) понимается всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.
Статистические гипотезы делятся на гипотезы о параметрах распределения известного вида (это так называемые параметрические гипотезы) и гипотезы о виде неизвестного распределения (непараметрические гипотезы).
Одну из гипотез выделяют в качестве основной (или нулевой) и обозначают 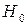 , а другую, являющуюся логическим отрицанием
, а другую, являющуюся логическим отрицанием 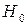 , т.е. противоположную
, т.е. противоположную 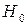 - в качестве конкурирующей (или альтернативной) гипотезы и обозначают
- в качестве конкурирующей (или альтернативной) гипотезы и обозначают 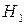 .
.
Гипотезу, однозначно фиксирующую распределение наблюдений, называют простой (в ней речь идет об одном значении параметра), в противном случае – сложной.
Например, гипотеза 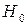 , состоящая в том, что математическое ожидание случайной величины
, состоящая в том, что математическое ожидание случайной величины  равно
равно 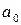 , то есть
, то есть 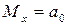 , является простой. В качестве альтернативной гипотезы можно рассматривать одну из следующих гипотез:
, является простой. В качестве альтернативной гипотезы можно рассматривать одну из следующих гипотез: 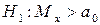 (сложная гипотеза),
(сложная гипотеза), 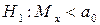 (сложная),
(сложная), 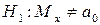 (сложная) или
(сложная) или 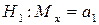 (простая гипотеза).
(простая гипотеза).
Имея две гипотезы 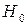 и
и 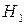 , надо на основе выборки
, надо на основе выборки 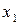 ,
, 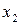 ,…,
,…, 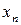 принять либо основную гипотезу
принять либо основную гипотезу 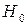 , либо конкурирующую
, либо конкурирующую 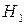 .
.
Правило, по которому принимается решение принять или отклонить гипотезу 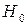 (соответственно отклонить или принять гипотезу
(соответственно отклонить или принять гипотезу 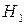 ), называется статистическим критерием (или просто критерием) проверки гипотезы
), называется статистическим критерием (или просто критерием) проверки гипотезы 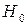 .
.
Проверку гипотез осуществляют на основании результатов выборки 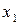 ,
, 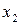 ,…,
,…, 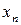 , из которых формируют функцию выборки
, из которых формируют функцию выборки 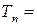
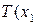 ,
, 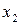 ,…,
,…, 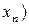 , называемой статистикой критерия.
, называемой статистикой критерия.
Основной принцип проверки гипотез состоит в следующем. Множество возможных значений статистики критерия 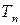 разбивается на два непересекающихся подмножества: критическую область
разбивается на два непересекающихся подмножества: критическую область 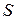 , то есть область отклонения гипотезы и область
, то есть область отклонения гипотезы и область 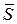 принятия этой гипотезы. Если фактически наблюдаемое значение статистики критерия (то есть значение критерия, вычисленное по выборке:
принятия этой гипотезы. Если фактически наблюдаемое значение статистики критерия (то есть значение критерия, вычисленное по выборке: 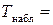
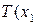 ,
, 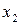 ,…,
,…, 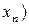 ) попадает в критическую область
) попадает в критическую область 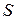 , то основная гипотеза
, то основная гипотеза 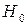 отклоняется и принимается альтернативная гипотеза
отклоняется и принимается альтернативная гипотеза 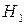 ; если же
; если же 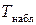 попадает в
попадает в 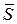 , то принимается
, то принимается 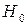 , а
, а 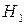 отклоняется.
отклоняется.
При проверке гипотезы может быть принято неправильное решение, то есть могут быть допущены ошибки двух родов:
Ошибка первого рода состоит в том, что отвергается нулевая гипотеза 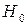 , когда на самом деле она верна.
, когда на самом деле она верна.
Ошибка второго рода состоит в том, что отвергается альтернативная гипотеза 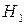 , когда она на самом деле верна.
, когда она на самом деле верна.
Рассматриваемые случаи наглядно иллюстрирует следующая таблица:
Гипотеза 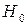
| Отвергается | Принимается |
| верна неверна | ошибка 1-го рода правильное решение | правильное решение ошибка 2-го рода |
Вероятность ошибки первого рода (обозначается через 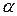 ) называется уровнем значимости критерия.
) называется уровнем значимости критерия.
Очевидно, 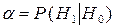 . Чем меньше
. Чем меньше 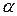 , тем меньше вероятность отклонить верную гипотезу. Допустимую ошибку первого рода обычно задают заранее.
, тем меньше вероятность отклонить верную гипотезу. Допустимую ошибку первого рода обычно задают заранее.
В одних случаях считается возможным пренебречь событиями, вероятность которых меньше 0,05 ( 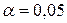 означает, что в среднем в 5 случаях из 100 испытаний верная гипотеза будет отвергнута), в других случаях, когда речь идет, например, о разрушении сооружений, гибели судна и т.п., нельзя пренебречь обстоятельствами, которые могут появиться с вероятностью, равной 0,001.
означает, что в среднем в 5 случаях из 100 испытаний верная гипотеза будет отвергнута), в других случаях, когда речь идет, например, о разрушении сооружений, гибели судна и т.п., нельзя пренебречь обстоятельствами, которые могут появиться с вероятностью, равной 0,001.
Обычно для 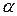 используются стандартные значения:
используются стандартные значения: 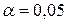 ;
; 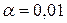 ; 0,005; 0,001.
; 0,005; 0,001.
Вероятность ошибки 2-го рода обозначается через 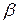 , то есть
, то есть 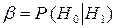 . Величину
. Величину 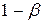 , то есть вероятность недопущения ошибки второго рода (отвергнуть неверную гипотезу
, то есть вероятность недопущения ошибки второго рода (отвергнуть неверную гипотезу 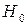 , принять верную
, принять верную 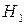 ) называется мощностью критерия.
) называется мощностью критерия.
Очевидно, 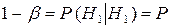
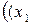 ,
, 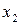 ,…,
,…, 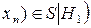 .
.
Чем больше мощность критерия, тем вероятность ошибки 2-го рода меньше, что, конечно, желательно (как и уменьшение 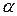 ).
).
Последствия ошибок 1-го, 2-го рода могут быть совершенно различными: в одних случаях надо минимизировать 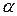 , в других -
, в других - 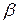 . Так, применительно к производству, к торговле, можно сказать, что
. Так, применительно к производству, к торговле, можно сказать, что 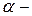 риск поставщика (то есть забраковка по выборке всей партии изделий, удовлетворяющих стандарту),
риск поставщика (то есть забраковка по выборке всей партии изделий, удовлетворяющих стандарту), 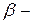 риск потребителя (то есть прием по выборке всей партии изделий, не удовлетворяющих стандарту); применительно к судебной системе, ошибка 1-го рода приводит к оправданию виновного, ошибка 2-го рода – к осуждению невиновного.
риск потребителя (то есть прием по выборке всей партии изделий, не удовлетворяющих стандарту); применительно к судебной системе, ошибка 1-го рода приводит к оправданию виновного, ошибка 2-го рода – к осуждению невиновного.
Отметим, что одновременное уменьшение ошибок 1-го и 2-го рода возможно лишь при увеличении объема выборок. Поэтому обычно при заданном уровне значимости 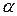 отыскивается критерий с наибольшей мощностью.
отыскивается критерий с наибольшей мощностью.
Методика проверки гипотез сводится к следующему:
1. Располагая выборкой 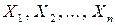 , формируют нулевую гипотезу
, формируют нулевую гипотезу 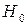 и альтернативную
и альтернативную 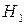 .
.
2. В каждом конкретном случае подбирают статистику критерия 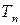
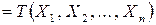 , обычно из нижеперечисленных:
, обычно из нижеперечисленных: 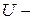 нормальное распределение,
нормальное распределение, 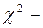 распределение хи-квадрат Пирсона,
распределение хи-квадрат Пирсона, 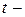 распределение Стьюдента.
распределение Стьюдента.
3. По статистике критерия 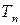 и уровню значимости
и уровню значимости 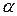 определяют критическую область
определяют критическую область 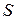 (и
(и 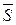 ). Для ее отыскания достаточно найти критическую точку
). Для ее отыскания достаточно найти критическую точку 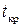 , то есть границу, отделяющую
, то есть границу, отделяющую 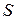 от
от 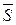 .
.
Границы областей определяются соответственно из соотношений:
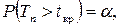 для правосторонней критической области
для правосторонней критической области 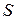 (рис. 5);
(рис. 5);
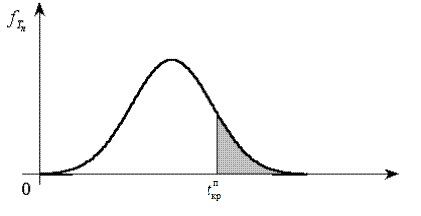
Рис. 5.Правосторонняя критическая область
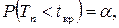 для левосторонней критической области
для левосторонней критической области 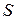 (рис. 6);
(рис. 6);
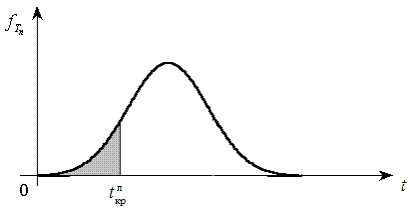
Рис. 6. Левосторонняя критическая область
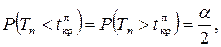 для двусторонней критической области
для двусторонней критической области 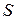 (рис. 7)
(рис. 7)
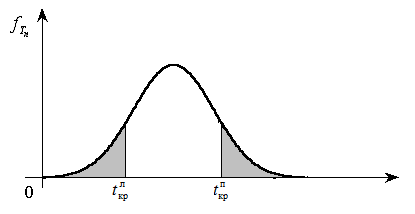
Рис. 7. Двусторонняя критическая область
Для каждого конкретного случая имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую приведенным выше соотношениям.
4. Для полученной реализации выборки 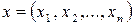 подсчитывают значение критерия, то есть
подсчитывают значение критерия, то есть 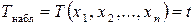 .
.
5. Если 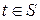 (например,
(например, 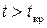 для правосторонней области
для правосторонней области 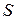 ), то нулевую гипотезу
), то нулевую гипотезу 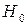 отвергают; если же
отвергают; если же 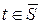 (
( 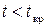 ), то нет оснований, чтобы отвергнуть гипотезу
), то нет оснований, чтобы отвергнуть гипотезу 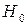 .
.
Дата добавления: 2016-04-22; просмотров: 2384;
