Коэффициент корреляции. Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции .

Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции .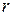

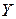Коэффициент корреляции между двумя случайными величинами и вычисляется по формуле:

,

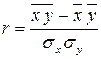где 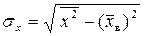, 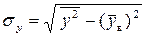- средние квадратические отклонения случайных величин 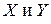соответственно.

Отметим некоторые свойства коэффициента корреляции:

1. Если 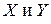независимые случайные величины, то коэффициент корреляции равен нулю.

2. Коэффициент корреляции принимает значения на отрезке 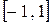, то есть 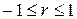. В зависимости от того, насколько 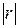приближается к 1, в математической статистике различают (шкала Шеддока): связи нет ( 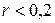), связь слабую ( 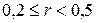), умеренную ( 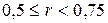), тесную 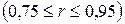и очень тесную .

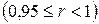3. Если 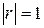, то между случайными величинами 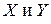имеет место функциональная, а именно линейная зависимость.

4. Коэффициент корреляции указывает на направление связи. Если 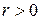, то связь прямая, если 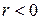отрицателен, то это свидетельствует о наличии обратной связи.

Квадрат коэффициента корреляции называется коэффициентом детерминации:

.

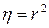Коэффициент детерминации 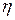показывает, какая часть общей вариации 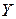обусловлена вариацией .

Пример 15. С целью анализа влияния заработной платы на текучесть рабочей силы на пяти однотипных предприятиях проведены измерения уровня зарплаты (тыс.руб.) и числа уволившихся за год рабочих :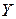

				5,5

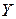
Определить степень влияния заработной платы на текучесть рабочей силы.

Решение.

Для определения тесноты связи вычислим коэффициент корреляции, для чего составим расчетную таблицу:

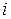
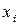
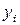
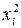
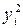
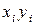
	5,5		30,25
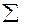
	23,5		116,25

Так как коэффициент корреляции рассчитывается по формуле

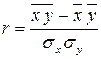, то:

1. Найдем средние значения: 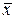(сумма значений второго столбца, деленная на число строк:

;

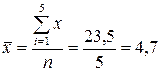среднее значение 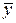(сумма значений третьего столбца, деленная на число строк):

;

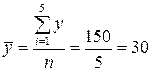среднее значение 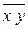(среднее значение шестого столбца):

.

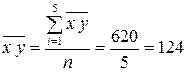2. Найдем средние квадратические отклонения :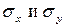

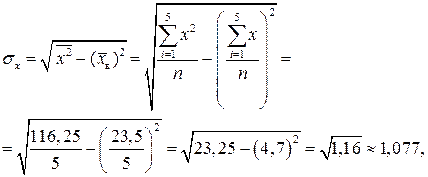
где 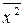рассчитывается как среднее значение четвертого столбца.

Аналогично ,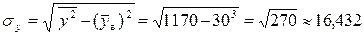

где 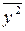- среднее значение пятого столбца.

3. Подставляя найденные значения в формулу коэффициента корреляции, получим:

.

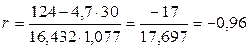Таким образом, можно сделать вывод, что связь между заработной платой и текучестью рабочей силы очень тесная и обратная, так как полученный коэффициент корреляции отрицательный. Это говорит о том, что чем меньше заработная плата ( 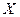), тем больше число уволившихся.

Выясним, какая часть вариации 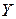обусловлена вариацией . Вычислим коэффициент детерминации:

.

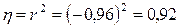То есть вариации текучести рабочей силы ( 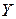) на 92% обусловлена вариацией заработной платы ( ).