Линейная парная регрессия.
После того, как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена степень тесноты, обычно переходят к математическому описанию вида зависимостей с использованием регрессионного анализа. Если коэффициент корреляции 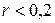 , то согласно шкале Шеддока связи между переменными нет, а следовательно не имеет смысла описывать модель связи.
, то согласно шкале Шеддока связи между переменными нет, а следовательно не имеет смысла описывать модель связи.
Регрессионная модель представляет собой математическое выражение, связывающее случайные величины 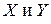 . Уравнение регрессии – это зависимость величины
. Уравнение регрессии – это зависимость величины 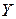 от
от  .
.
Часто встречающейся моделью зависимости является линейная парная корреляция. Вообще говоря, уравнение регрессии может описывать взаимосвязь не двух, а более переменных (то есть быть не парной, а множественной). Кроме того, связь между переменными далеко не всегда линейна.
В общем случае уравнение регрессии имеет вид:
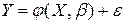 ,
,
где 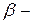 параметры модели,
параметры модели, 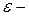 ошибка наблюдений,
ошибка наблюдений, 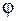 произвольная функция.
произвольная функция.
Уравнение парной линейной регрессии выглядит следующим образом:
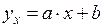 ,
,
где  и
и 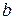 - параметры уравнения линейной регрессии.
- параметры уравнения линейной регрессии.
Для нахождения параметром применяют метод наименьших квадратов, согласно которому неизвестные  и
и 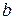 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических средних значений от значений, найденных по уравнению регрессии была минимальной:
выбираются таким образом, чтобы сумма квадратов отклонений эмпирических средних значений от значений, найденных по уравнению регрессии была минимальной:
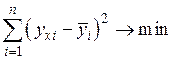 .
.
Получим систему нормальных уравнений для нахождения искомых параметров:
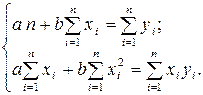
Разделив обе части уравнений на 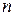 , получим систему нормальных уравнений в виде:
, получим систему нормальных уравнений в виде:
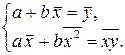
Решая систему уравнений, найдем:
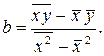
зная, что 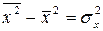 и формулу для вычисления коэффициента корреляции можем записать:
и формулу для вычисления коэффициента корреляции можем записать:
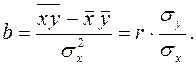
Коэффициент 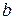 называется коэффициентом регрессии. Он показывает, на сколько единиц в среднем изменяется переменная
называется коэффициентом регрессии. Он показывает, на сколько единиц в среднем изменяется переменная 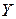 при изменении
при изменении  на одну единицу.
на одну единицу.
Замечание. Знак коэффициента регрессии указывает на направление связи: если 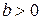 , связь прямая, если
, связь прямая, если 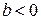 - обратная. Очевидно, что знаки коэффициентов корреляции и регрессии должны совпадать.
- обратная. Очевидно, что знаки коэффициентов корреляции и регрессии должны совпадать.
Решая систему относительно параметра  , получим:
, получим:
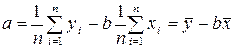 .
.
Для установления влияния на зависимую переменную независимой переменной, то есть для интерпретации модели используется коэффициент эластичности:
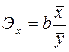 .
.
Коэффициент эластичности показывает, на сколько процентов изменится 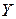 при изменении
при изменении  на 1 %.
на 1 %.
Вывод
Пример 16. В условиях предыдущей задачи найти уравнение линейной регрессии, выражающее зависимость между заработной платой рабочих и числом уволившихся.
Решение.
1. Для определения параметров  и
и 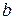 линии регрессии
линии регрессии 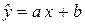 составим систему нормальных уравнений:
составим систему нормальных уравнений:
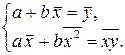
2. Подставляя найденные в предыдущей задаче средние значения 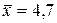 ,
, 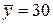 ,
, 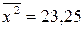
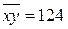 , получим:
, получим:
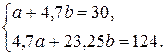
3. Решая эту систему, найдем 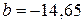 ;
; 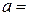 98,85. Тогда уравнение регрессии:
98,85. Тогда уравнение регрессии:
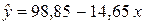 .
.
Отрицательный коэффициент регрессии подтверждает то, что связь между заработной платой рабочих и текучестью кадров обратная. Вычислим коэффициент эластичности:
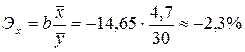 .
.
Полученный коэффициент свидетельствует о том, что при увеличении заработной платы на 1%, число увольняющихся в среднем сократиться на 2,3%.
Пример выполнения контрольной работы
Задание 1. В результате статистического исследования, проведенного среди работников некоторого промышленного объединения на основе случайной выборки, получены следующие данные о величине совокупного месячного дохода (тыс. руб.)
| 1,806 | 10,530 | 7,540 | 5,347 | 4,601 | 6,115 | 2,189 | 6,992 | 5,479 | 3,829 |
| 4,519 | 3,188 | 4,496 | 7,868 | 5,201 | 7,337 | 7,293 | 4,439 | 2,712 | 3,283 |
| 6,370 | 3,324 | 4,891 | 3,830 | 3,782 | 5,703 | 6,135 | 4,537 | 8,074 | 3,942 |
| 8,025 | 4,685 | 3,749 | 4,582 | 6,580 | 5,430 | 6,252 | 6,928 | 6,508 | 6,377 |
| 7,602 | 3,852 | 5,564 | 4,005 | 3,954 | 4,185 | 4,324 | 0,502 | 5,958 | 4,869 |
Выполнить статистическую обработку полученных данных.
Решение.
1. Для полученной выборочной совокупности объемом 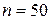 :
:
а). Производим ранжирование выборочных данных.
| 0,502 | 1,806 | 2,189 | 2,712 | 3,188 | 3,283 | 3,324 | 3,749 | 3,782 | 3,829 |
| 3,830 | 3,852 | 3,942 | 3,954 | 4,005 | 4,185 | 4,324 | 4,439 | 4,496 | 4,519 |
| 4,537 | 4,582 | 4,601 | 4,685 | 4,869 | 4,891 | 5,201 | 5,347 | 5,430 | 5,479 |
| 5,564 | 5,703 | 5,958 | 6,115 | 6,135 | 6,252 | 6,370 | 6,377 | 6,508 | 6,580 |
| 6,928 | 6,992 | 7,293 | 7,540 | 7,602 | 7,868 | 8,025 | 8,074 | 8,337 | 10,530 |
б) Определяем минимальное и максимальное значение признака.
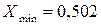 тыс.руб.;
тыс.руб.; 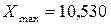 тыс.руб.
тыс.руб.
в) Находим размах варьирования признака
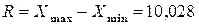 тыс.руб.
тыс.руб.
г) Определяем число групп, на которые разбиваем выборочную совокупность (округление проводим до ближайшего целого)
k 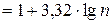 =7.
=7.
д) Определяем длину интервала по формуле
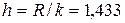
е) Определяем границы интервалов и группируем данные по соответствующим интервалам. Границы интервалов ( 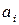 ,
, 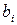 ), i=1,2,…,k, получаем следующим образом
), i=1,2,…,k, получаем следующим образом
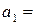
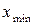 ;
; 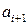
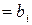
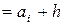 +h;
+h; 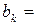
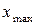 .
.
Замечание. В данном случае за начало первого интервала принимаем 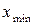 , так как если воспользоваться формулой
, так как если воспользоваться формулой 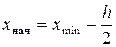 , то получим
, то получим 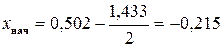 , что не имеет экономического смысла, то есть при определении границ интервала не стоит забывать об экономическом содержании задачи.
, что не имеет экономического смысла, то есть при определении границ интервала не стоит забывать об экономическом содержании задачи.
В процессе группировки определяем количество вариант, удовлетворяющих неравенствам 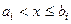 , и строим интервальный вариационный ряд путем заполнения таблицы:
, и строим интервальный вариационный ряд путем заполнения таблицы:
| № интервала | Границы интервала
 - - 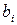
| Частота 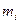
| Накопленная частота 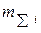
|
| 0,502-1,935 | |||
| 1,935-3,367 | |||
| 3,367-4,800 | |||
| 4,800-6,232 | |||
| 6,232-7,665 | |||
| 7,665-9,097 | |||
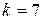
| 9,097-10,530 | ||
| - | - |
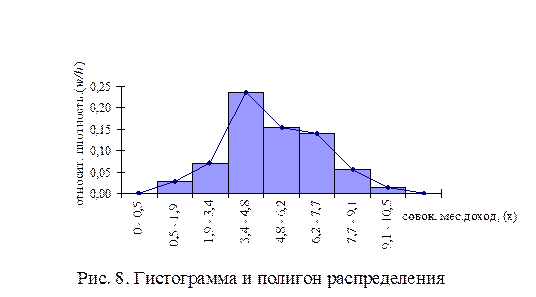
ж) На основе полученных данных строим статистический ряд распределения и его геометрические представления.
В пределах каждого интервала все значения признака приравниваем к его серединному значению ( 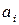 +
+ 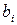 )/2 и считаем, что частота относится именно к этому значению. Необходимые вычисления производим в таблице:
)/2 и считаем, что частота относится именно к этому значению. Необходимые вычисления производим в таблице:
| № Интер вала | Интервалы
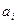 - - 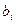
| 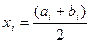
| Частости
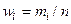
| Накопленные
частости 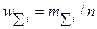
| Относительная
плотность распределения 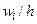
|
| 0,502-1,935 | 1,218 | 0,04 | 0,04 | 0,028 | |
| 1,935-3,367 | 2,651 | 0,1 | 0,14 | 0,070 | |
| 3,367-4,800 | 4,083 | 0,34 | 0,48 | 0,237 | |
| 4,800-6,232 | 5,516 | 0,22 | 0,7 | 0,154 | |
| 6,232-7,665 | 6,949 | 0,2 | 0,9 | 0,140 | |
| 7,665-9,097 | 8,381 | 0,08 | 0,98 | 0,056 | |
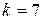
| 9,097-10,530 | 9,814 | 0,02 | 0,014 | |
| __ | __ | 1,00 | __ | __ |
Статистический ряд распределения образуют данные 2-го и 3-го столбцов таблицы. Для построения гистограммы распределения используются данные 1-го и 5-го столбцов, полигона -2-го и 5-го столбцов, кумуляты (функции распределения)– данные 1-го и 4-го столбцов.
Напомним, что для построения гистограммы по оси абсцисс откладываются частичные интервалы ( 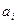 ,
, 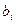 ), на каждом из которых строим прямоугольник высотой
), на каждом из которых строим прямоугольник высотой 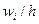 . Площадь ступенчатой фигуры, образуемой гистограммой, равна единице. Соединяя середины верхних оснований прямоугольников отрезками прямой, из гистограммы можно получить полигон распределения (рис. 8).
. Площадь ступенчатой фигуры, образуемой гистограммой, равна единице. Соединяя середины верхних оснований прямоугольников отрезками прямой, из гистограммы можно получить полигон распределения (рис. 8).
При построении кумуляты в точках, соответствующих правому концу интервалов, по оси ординат откладываются накопленные частности 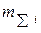 , которые затем соединяются ломаной линией (рис.9)
, которые затем соединяются ломаной линией (рис.9)
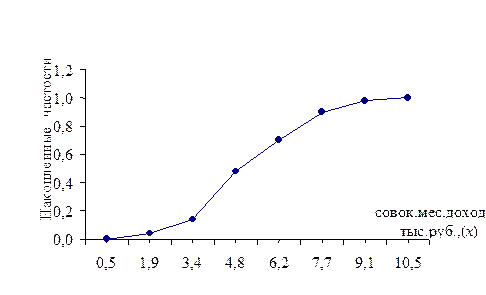
Рис 9. Кумулята распределения
2. Найдем выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки, моду и медиану.
а) Вначале находим выборочное среднее, характеризующее центр распределения, около которого группируются выборочные данные, как взвешенное среднее
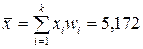 тыс.руб.
тыс.руб.
Обозначая далее 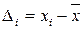 , где
, где 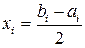 , вычисляем отклонения
, вычисляем отклонения 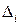 варианты
варианты 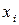 от среднего значения
от среднего значения 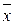 и заполняем таблицу:
и заполняем таблицу:
| № п./п. | 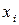
| 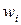
| 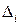
| 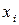 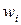
| 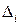 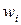
| 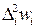
|
| 1,218 | 0,04 | -3,954 | 0,049 | -0,158 | 0,625 | |
| 2,651 | 0,10 | -2,521 | 0,265 | -0,252 | 0,636 | |
| 4,083 | 0,34 | -1,089 | 1,388 | -0,370 | 0,403 | |
| 5,516 | 0,22 | 0,344 | 1,214 | 0,076 | 0,026 | |
| 6,949 | 0,20 | 1,776 | 1,390 | 0,355 | 0,631 | |
| 8,381 | 0,08 | 3,209 | 0,670 | 0,257 | 0,824 | |
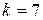
| 9,814 | 0,02 | 4,642 | 0,196 | 0,093 | 0,431 |
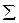
| - | 1,00 | - | 5,172 | 0,000 | 3,576 |
Дисперсия выборочного распределения: 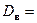
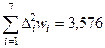 .
.
Среднее квадратическое отклонение 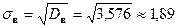 .
.
В данном распределении модальным является интервал (3,367 – 4,800), так как ему соответствует наибольшая частота ( 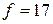 ). Значение моды определим по формуле:
). Значение моды определим по формуле:
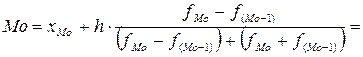
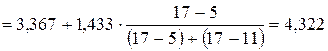 .
.
Место медианы 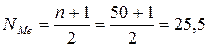 , поэтому медианным является интервал (4,800 – 6,232), так как в этом интервале находятся номера 25 и 26. Вычислим медиану:
, поэтому медианным является интервал (4,800 – 6,232), так как в этом интервале находятся номера 25 и 26. Вычислим медиану:
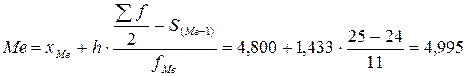 .
.
3. Проверим гипотезу о соответствии имеющего статистического распределения нормальному закону.
Число наблюдений в крайних интервалах меньше 5, поэтому объединяем их с соседними. Получим:
| Интервал | 0,502 – 3,367 | 3,367 – 4,800 | 4,800 – 6,232 | 6,232 – 7,665 | 7,665 – 10,530 |
Частота , 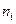
|
Оценки параметров распределения вычислим по выборке:
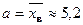 ;
; 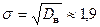
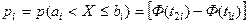 ,
,
где 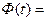
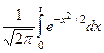 ,
, 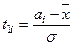 ,
, 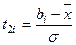 .
.
Плотность распределения вероятностей теоретического распределения на каждом интервале 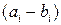 рассчитывается по формуле
рассчитывается по формуле 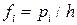 .
.
Расчеты выполним в табличной форме:
| № п./п. | Интервалы
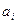 - - 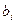
| 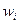
| 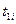
| 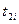
| 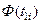
| 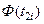
| 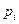
| 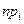
| 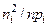
|
| 0,502-3,367 | 0,14 | 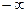
| -0,96 | -0,500 | -0,3315 | 0,1685 | 8,425 | 5,82 | |
| 3,367-4,800 | 0,34 | -0,96 | -0,21 | -0,3315 | -0,0832 | 0,2483 | 12,415 | 23,28 | |
| 4,800-6,232 | 0,22 | -0,21 | 0,54 | -0,0832 | 0,2054 | 0,2886 | 14,43 | 8,39 | |
| 6,232-7,665 | 0,20 | 0,54 | 1,30 | 0,2054 | 0,4032 | 0,1978 | 9,89 | 10,11 | |
| 7,665-10,530 | 0,10 | 1,30 | 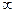
| 0,4032 | 0,500 | 0,0968 | 4,84 | 5,17 | |
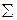
| - | 1,00 | - | - | - | - | 1,000 | 52,76 |
Вычисляем наблюдаемое значение критерия 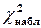 :
:
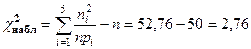 .
.
Число степеней свободы по выборке равно 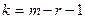 , где
, где  число интервалов,
число интервалов, 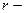 число параметров распределения, в нашем случае:
число параметров распределения, в нашем случае:
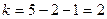 .
.
При уровне значимости 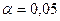 и
и 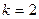 по таблице распределения
по таблице распределения 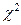 находим
находим 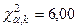 . Так как
. Так как 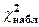
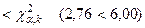 , то нет оснований отвергнуть выдвинутую гипотезу.
, то нет оснований отвергнуть выдвинутую гипотезу.
4. Точечная оценка математического ожидания найдена при проверке гипотезы о соответствии распределения нормальному закону: 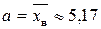 (метод моментов).
(метод моментов).
Доверительный интервал для математического ожидания при известной дисперсии определяется из неравенства:
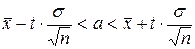 ,
,
где 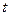 определяется из уравнения
определяется из уравнения 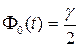 .
.
Учитывая, что 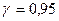 , получаем
, получаем 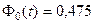 . По таблице находим
. По таблице находим 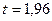 . Тогда
. Тогда 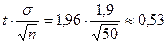 . Доверительный интервал для математического ожидания будет:
. Доверительный интервал для математического ожидания будет:
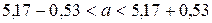
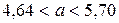 , то есть
, то есть 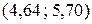 .
.
Задание 2. Имеются следующие данные о расходе бензина автомобилями некоторой марки:
| Мощность двигателя, л.с. | Расход бензина, л. /100км. | Мощность двигателя, л.с. | Расход бензина, л. /100км. |
| 9,5 5,7 9,0 6,1 14,5 6,0 17,4 8,0 7,3 22,0 | 12,7 13,0 18,0 11,0 12,6 17,5 16,1 19,7 10,2 15,0 |
Требуется:
1. Оценить степень зависимости между переменными;
2. Найти уравнение линейной регрессии;
3. Интерпретировать полученную модель, сделать выводы.
Решение.
1. Для определения тесноты связи вычислим коэффициент корреляции, для чего составим расчетную таблицу:
| 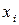
| 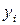
| 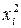
| 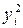
| 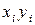
|
| 6,0 | 36,00 | 504,0 | |||
| 5,7 | 32,49 | 495,9 | |||
| 6,1 | 37,21 | 549,0 | |||
| 7,3 | 53,29 | 722,7 | |||
| 8,0 | 64,00 | 840,0 | |||
| 9,5 | 90,25 | 1045,0 | |||
| 9,0 | 81,00 | 1035,0 | |||
| 11,0 | 121,00 | 1375,0 | |||
| 10,2 | 104,04 | 1346,4 | |||
| 12,6 | 158,76 | 1764,0 | |||
| 12,7 | 161,29 | 1816,1 | |||
| 13,0 | 169,00 | 1950,0 | |||
| 14,5 | 210,25 | 2320,0 | |||
| 15,0 | 225,00 | 2475,0 | |||
| 16,1 | 259,21 | 2817,5 | |||
| 17,4 | 302,76 | 3306,0 | |||
| 17,5 | 306,25 | 3500,0 | |||
| 18,0 | 324,00 | 3690,0 | |||
| 19,7 | 388,09 | 4334,0 | |||
| 22,0 | 484,00 | 5280,0 | |||
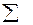
| 251,3 | 3607,89 | 41165,6 |
Коэффициент корреляции рассчитывается по формуле:
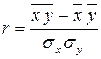 .
.
а) Найдем средние значения:
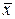 (сумма значений второго столбца, деленная на число строк:
(сумма значений второго столбца, деленная на число строк:
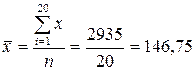 ;
;
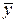 (сумма значений третьего столбца, деленная на число строк):
(сумма значений третьего столбца, деленная на число строк):
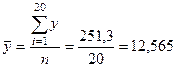 ;
;
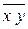 (среднее значение шестого столбца):
(среднее значение шестого столбца):
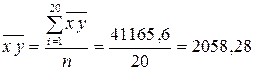 .
.
б) Найдем средние квадратические отклонения 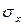 и
и 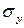 :
:
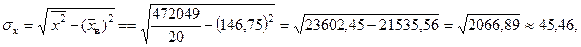
где 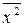 рассчитывается как среднее значение четвертого столбца.
рассчитывается как среднее значение четвертого столбца.
Аналогично 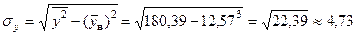 ,
,
где 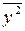 - среднее значение пятого столбца.
- среднее значение пятого столбца.
в) Подставляя найденные значения в формулу коэффициента корреляции, получим:
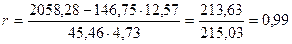 .
.
2. Найдем уравнение линейной регрессии.
а) Для определения параметров 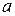 и
и 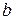 линии регрессии
линии регрессии 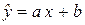 составим систему нормальных уравнений:
составим систему нормальных уравнений:
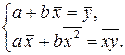
б) Подставляя найденные в предыдущем пункте задачи средние значения 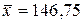 ,
, 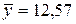 ,
, 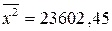 ,
, 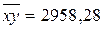 , получим:
, получим:
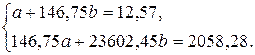
в). Решая эту систему, найдем 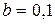 ;
; 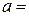 -2,11. Тогда уравнение регрессии имеет вид:
-2,11. Тогда уравнение регрессии имеет вид:
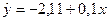 .
.
3. Таким образом, можно сделать вывод, что связь между мощностью двигателя и расходом бензина прямая и очень тесная, так как полученный коэффициент корреляции положительный и очень близок к единице. Это говорит о том, что чем больше мощность двигателя ( 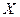 ), тем больше расход бензина (
), тем больше расход бензина ( 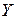 ).
).
Выясним, какая часть вариации 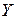 обусловлена вариацией
обусловлена вариацией 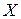 , для этого вычислим коэффициент детерминации:
, для этого вычислим коэффициент детерминации:
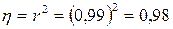 .
.
То есть вариация расхода бензина ( 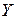 ) на 98% обусловлена вариацией мощности двигателя (
) на 98% обусловлена вариацией мощности двигателя ( 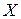 ).
).
Положительный коэффициент регрессии 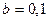 подтверждает то, что связь между мощностью двигателя и расходом топлива прямая. Вычислим коэффициент эластичности:
подтверждает то, что связь между мощностью двигателя и расходом топлива прямая. Вычислим коэффициент эластичности:
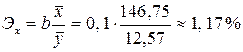 .
.
Полученный коэффициент свидетельствует о том, что при увеличении мощности двигателя на 1%, расход бензина в среднем увеличится на 1,17 %.
Дата добавления: 2016-04-22; просмотров: 4099;
