Определение расстояния между точкой и плоско плоскостью.
ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ ЭПЮРОВ (ЧЕРТЕЖЕЙ)
ЭПЮР 2
Целевое назначение. Закрепление знаний студентов по способам преобразования эпюра.
Содержание работы.. Даны координаты вершин пирамиды SABС.
Определить:
- истинную величину основания ABC;
- расстояние от вершины S до плоскости основания ABC;
-кратчайшее расстояние между ребрами SA и ВС;
- величину двугранного угла при ребре АВ.
Методические указания к выполнению эпюра №2
Индивидуальные задания по вариантам приведены в приложении А1.
Задачи на эпюре должны быть решены следующими способами:
- вращения вокруг оси перпендикулярной плоскости проекции;
- плоскопараллельного перемещения;
- вращения вокруг горизонтали или фронтали;
-перемены плоскостей проекций.
Студент должен самостоятельно выбрать наиболее рациональный способ решения каждой задачи, но так, чтобы обязательно были применены на эпюре все указанные способы.
Эпюр должен быть выполнен в соответствии с ГОСТами Единой системы конструкторской документации (ЕСКД)/2/ и отличаться выразительностью и опрятностью графического решения поставленных задач. Под выразительностью в данном случае понимают те свойства чертежа, которые облегчают процесс чтения.
- Эпюр студенты выполняют на листе чертежной бумаги формата А3 (297X420 мм). Запрещается применять для выполнения эпюров кальку и другую прозрачную и тонкую бумагу.
- Эпюры должны быть выполнены по размерам, указанным в заданиях, в масштабе 1:1.
- Толщина и тип линий должны быть приняты в соответствии с ГОСТ 2.303—68*, «Линии». Условия задач, все построения и искомые элементы на эпюре следует выполнять с помощью чертежных инструментов карандашом, вначале тонкими линиями толщиной приблизительно 0,3 мм в целях достижения точности построения.
При обводке чертежа рекомендуются следующие толщины и типы линий:
-линии видимого контура — сплошные, толщиной 0,8—1,0 мм;
-линии невидимого контура — штриховые, толщиной 0,4—0,5 мм;
-линии рамки поля чертежа и штампа — сплошные, толщиной 0,4—0,5 мм.
Все остальные линии — тонкие толщиной приблизительно 0,3 мм.
4. Обводить эпюр следует черным и цветными карандашами. Условие задачи и все построения выполняют черным карандашом, искомые линии — цветными (красными или синими).
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Трудоемкость и, как следствие, точность графического решения задач часто зависят не только от сложности задач, но и от того, какое положение занимают геометрические фигуры, входящие в условия задачи, по отношению к плоскостям проекций.
Проиллюстрируем сказанное примерами.
Определение расстояния между точкой и плоско плоскостью.
Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опушенного из точки на плоскость.
Поэтому решение этой задачи состоит из последовательного выполнения следующих графических операций:
1) из точки А опускаем перпендикуляр l на плоскость a;
2) находим точку М пересечения этого перпендикуляра с плоскостью
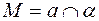 ;
;
3) определяем длину отрезка [AM].
Если плоскость a общего положения, то для того чтобы пустить на эту плоскость перпендикуляр, необходимо предварительно определить направление проекций горизонтали и фронтали этой плоскости. Нахождение точки встречи этого перпендикуляра с плоскостью также требует выполнения дополнительных геометрических построений. Решение задачи упрощается, если плоскость a занимает частное положение относительно плоскостей проекций. В этом случае и проведение проекций перпендикуляра, и нахождение точки его встречи с плоскостью осуществляется без каких-либо дополнительных вспомогательных построений.
ПРИМЕР 1. Определить расстояние от точки А до фронтально проецирующей a (рис.1).
Решение. Через 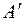 проводим горизонтальную проекцию перпендикуляра
проводим горизонтальную проекцию перпендикуляра 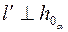 ,а через А"- его фронтальную проекцию
,а через А"- его фронтальную проекцию 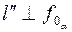 . Отмечаем точку B" =
. Отмечаем точку B" = 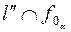 . Так как
. Так как 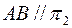 , то
, то 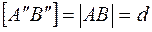 .
.
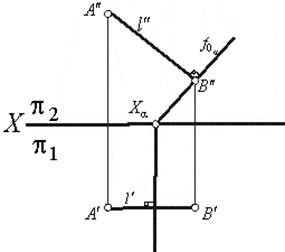 |
Рис.1
Из рассмотренного примера видно, насколько просто решается задача, когда плоскость занимает проецирующее положение. Поэтому, если в исходных данных будет задана плоскость общего положения, то, прежде чем приступить к решению, следует перевести плоскость в положение, перпендикулярное к какой-либо плоскости проекции.
Приведенные примеры показывают, что проецируемая фигура может занимать по отношению к плоскости проекции или произвольное, или частное положение. В первом случае, как правило, получаются проекции, неудобные для решения задач. В то же время решение задачи значительно упрощается, когда мы имеем дело с частным расположением геометрических фигур относительно плоскости проекции. Наиболее выгодным частным положением проецируемой фигуры (в случае ортогонального проецирования), при котором получаются проекции фигуры, удобные для решения задач, следует считать:
а) положение, перпендикулярное к плоскости проекции, — при решении позиционных задач;
б) положение, параллельное плоскости проекции, — для решения метрических задач.
В связи с этим, естественно, возникает вопрос, каким путем можно получить удобные проекции для решения поставленной задачи по заданным неудобным ортогональным проекциям?
Переход от общего положения геометрической фигуры к частному можно осуществить изменением взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями:
во-первых, перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве;
во-вторых, выбором новой плоскости проекции, по отношению к которой проецируемая фигура, не меняющая своего положения в пространстве, окажется в частном положении.
Первый путь лежит в основе способа плоскопараллельного перемещения; второй — составляет теоретическую базу способа замены плоскостей проекций.
Дата добавления: 2016-04-14; просмотров: 1571;
