Проекции (совмещение)

Совмещение является частным случаем вращения плоскости вок­руг горизонтали и фронтали. При совмещении за ось вращения при­нимается не произвольная горизонталь или фронталь плоскости, а ее горизонтальный или фронтальный след (нулевые горизонталь или фрон­таль). В этом случае в результате поворота плоскости она совпадает (совмещается) с плоскостью проекции 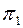, если вращение осуществляет­ся вокруг горизонтального следа плоскости, либо с при вращении вокруг ее фронтального следа.

Рис.11

Совмещение так же, как и вращение, вокруг горизонтали или фронта­ли, применяется, когда требуется определить истинный вид фигур, принадлежащих плоскости, или построить в плоскости общего положе­ния фигуру заданной формы и размеров.

Сущность способа совмещения можно уяснить из рассмотрения рис. 12,а. Плоскость общего положения a вращается вокруг следа 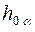до совпадения ее с горизонтальной плоскостью проекции. При этом преобра­зовании след 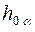, как ось вращения, останется на месте. Поэтому для нахождения совмещенного положения плоскости достаточно найти совмещенное положение только одной принадлежащей ей точки (не лежащей на следе ).

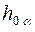В качестве такой точки целесообразно (для упрощения графических построений) взять точку А, принадлежащую фронтальному следу.

Точка А (А'А") при вращении вокруг оси 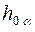будет перемещать­ся по дуге окружности, принадлежащей плоскости b, перпендикулярной к оси вращения.

а) б)

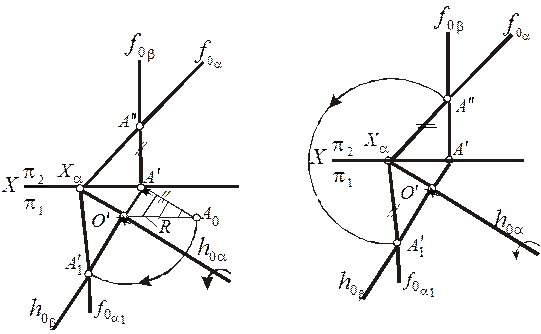
Рис.12

Графические построения, которые необходимо выполнить на эпю­ре Монжа для определения положения точки А, приведены на рис.12,а (как видно из рисунка, они аналогичны построениям, выполненным на рис. 11). Совмещенное с плоскостью проекции положение фрон­тального следа 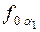определяется точками .

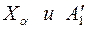Следует иметь в виду, что любая геометрическая фигура плоскости a при ее совмещении с плоскостью проекции 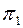проецируется в конгруэнтную фигуру. Поэтому 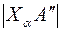, указывающий расстояние от точки схода следов Х_а до А", принадлежащей фронтальному следу, конгруэнтен 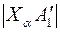на совмещенном положении следа 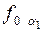. В связи с этим положение точки 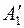, а следовательно, и следа 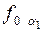мож­но определить, не пользуясь центром и радиусом вращения. Для этого достаточно из точки Х_а (рис. 12,6) описать дугу радиусом, равным расстоянию 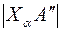, до ее пересечения с прямой (горизонтальным сле­дом 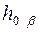плоскости b, в кото­рой будет перемещаться точка А), проведенной через А' пер­пендикулярно к 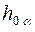. Через по­лученную точку пройдет фрон­тальный след плоскости 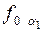при совмещении его с плоскостью .

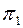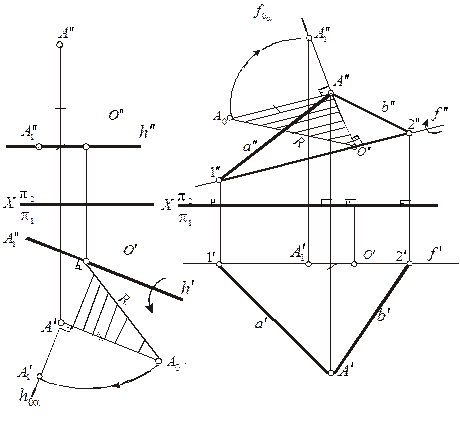
Рассмотрим часто решаемую задачу по определению величину уг­лов 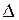ABC (рис. 13).

РЕШЕНИЕ. Вращаем плоскость 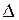АВС вокруг фронтали f этого треугольника до положения, параллельного плоскости 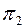. Через вершину А 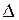АВС проводим фронталь 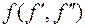. Точки А и D как при­надлежащие оси вращения не изменят своего положения в процессе преобразо­вания. Поэтому, достаточно повернуть только одну точку. На рис. 13 в качестве такой точки взята вершина В 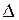АВС.

Вершина треугольника С при враще­нии вокруг фронтали будет перемещать­ся по дуге окружности, плоскость кото­рой перпендикулярна оси вращения f; поэтому фронтальная проекция этой окружности перпендикулярна f" и новое положение 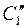определится в точке пересечения этого перпендикуляра с новым положением прямой 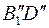. После такого поворота плоскость треугольника переводится в положение, параллельное плоскости 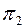.Следовательно, на основа­нии инвариантного свойства 2д (см. § 6)/1/ углы при вершинах 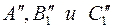проеци­руются без искажения.